Question

Найдите объём пирамиды, в основании которой лежит прямоугольный треугольник с катетами 3 и 4 см, а каждое боковое ребро образует с плоскостью основания угол 45°

Answer 1

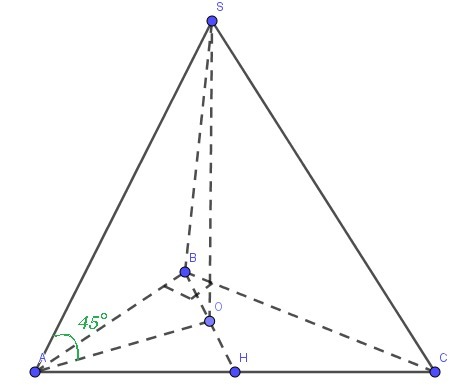
Рассмотрим основание. Основанием пирамиды есть прямоугольный треугольник ABC, в нём AB = 3 см и BC = 4 см, тогда по т. Пифагора

$mathrm{AC=sqrt{AB^2+BC^2}=5}$ см.

OA - радиус описанной окружности и равен он половине гипотенузы.

OA = AC/2 = 5/2 см.

Рассмотрим прямоугольный треугольник SOA, в нём ∠SAO=45°, тогда ∠ASO=90°-∠SAO = 90° - 45° = 45°, следовательно, треугольник SOA равнобедренный прямоугольный треугольник: SO = OA = 5/2 см.

Объем: $mathrm{V=frac{1}{3} S_{oc_H}h=frac{1}{3}cdotfrac{3cdot 4}{2}cdotfrac{5}{2}=5}$ см³

Ответ: 5 см³.