Question

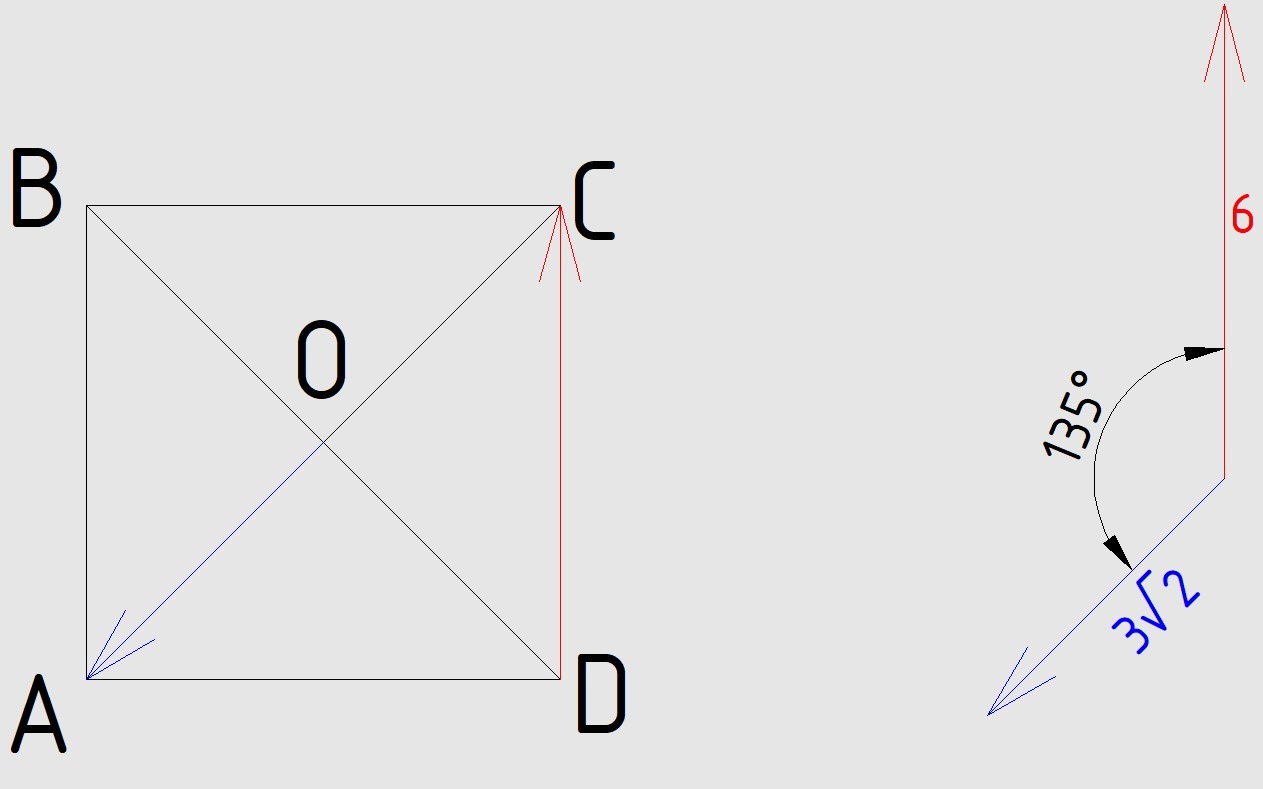
В квадрате авсд сторона равна 6. Диагонали пересекаются в точке о.
Найдите скалярное произведение векторов дс и оа

Answer 1

длина диагонали квадрата по теореме Пифагора
АС² = АВ² + ВС²
АС² = 6² + 6² = 2*36
АС = √(2*36) = 6√2
АО - половина диагонали
АО = 6√2/2 = 3√2
и скалярное произведение
ДС·ОА = |ДС|*|ОА|*cos(β) = 6*3√2*cos(135°) = 18√2*(-1/√2) = -18