А) Решите уравнение tg^3x+tg^2x-3tgx-3=0
б) Укажите корни этого уравнения на интервале [2п;7п/2]
Пожалуста, очень нужно...
Ответы
Ответ дал:
0
б)
отбор корней на картиночке
Ответ: a)
б)
Приложения:
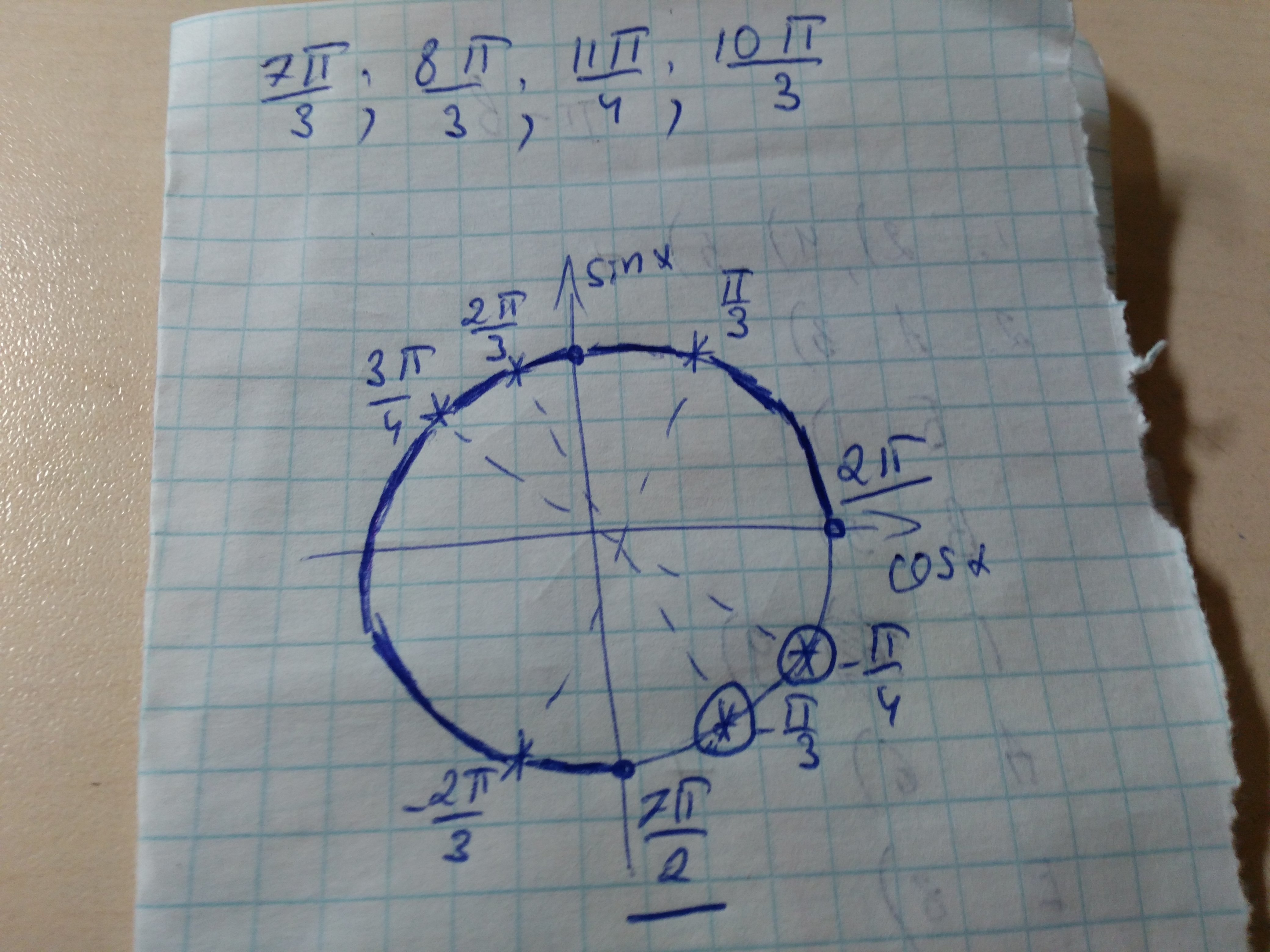
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад