Question

20БАЛЛОВ Диагональ боковой грани правильной треугольной призмы равна d и образует с диагональю боковой грани, которая выходит из той же вершины, угол β. Найдите площадь полной поверхности призмы.

Answer 1

Ответ:

$d^{2}sqrt{3(1-cosbeta )}(sqrt{12cosbeta -6}+sqrt{1-cosbeta })$

Объяснение:

S = Sполн = Sбок + 2Sabc

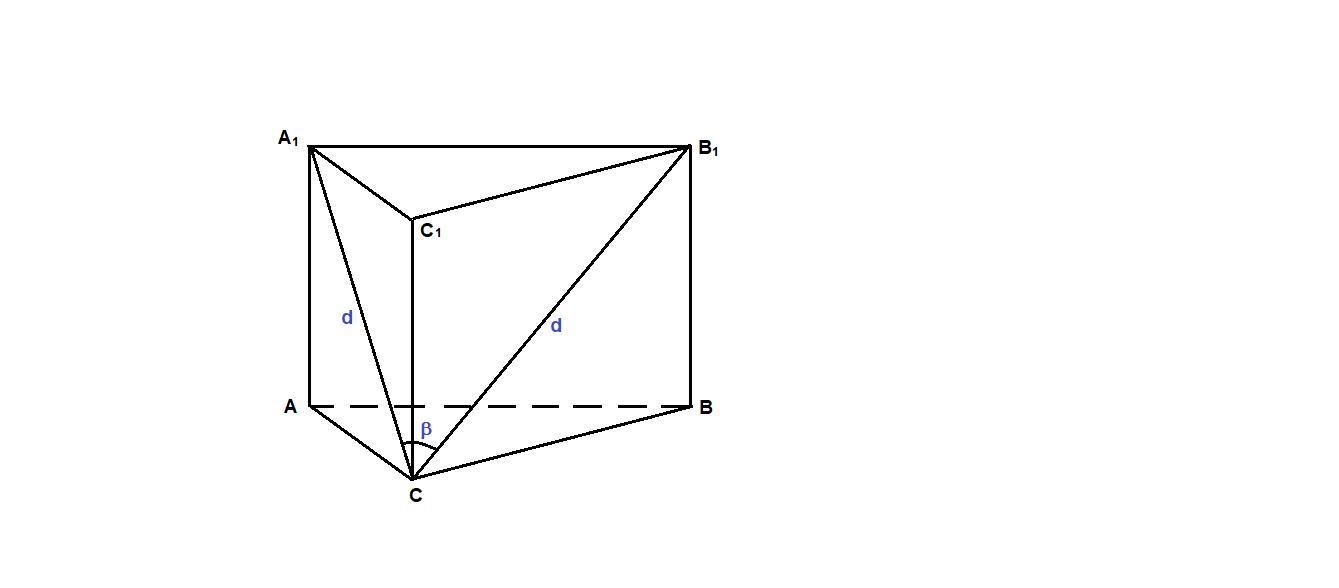
Из ΔА₁СВ₁ по теореме косинусов найдем сторону основания:

A₁B₁² = d² + d² - 2 · d · d · cosβ = 2d² - 2d²cosβ=2d²(1 - cosβ)

$A_{1}B_{1}=dsqrt{2(1-cosbeta )}$

Из ΔАА₁С по теореме Пифагора найдем высоту:

$AA_{1}=sqrt{d^{2}-AC^{2}}=sqrt{d^{2}-2d^{2}(1-cosbeta )}=dsqrt{1-2+2cosbeta }=dsqrt{2cosbeta -1}$

Sбок = Pосн · h

Sбок = $3dsqrt{2(1-cosbeta )}cdot dsqrt{2cosbeta -1}=3d^{2}sqrt{2(1-cosbeta )(2cosbeta -1)}$

$S_{ABC}=dfrac{A_{1}B_{1}^{2}sqrt{3}}{4}=dfrac{2d^{2}(1-cosbeta )sqrt{3}}{4}=dfrac{d^{2}sqrt{3}(1-cosbeta )}{2}$

$S=3d^{2}sqrt{2(1-cosbeta )(2cosbeta -1)}+2cdot dfrac{d^{2}sqrt{3}(1-cosbeta )}{2}$

$S=3d^{2}sqrt{2(1-cosbeta )(2cosbeta -1)}+d^{2}sqrt{3}(1-cosbeta )$

$S=d^{2}sqrt{3(1-cosbeta )}(sqrt{12cosbeta -6}+sqrt{1-cosbeta })$