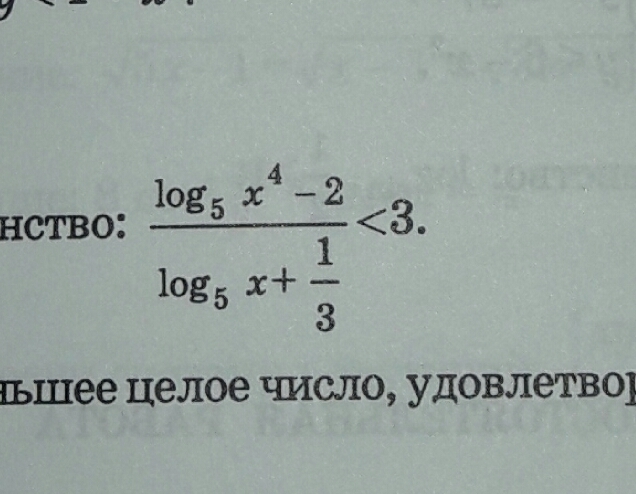Question

Решите неравенство...

Answer 1

$frac{log_5x^4-2}{log_5x+ frac{1}{3} } textless 3 \ \ frac{log_5x^4-2}{log_5x+ frac{1}{3} } -3 textless 0 \ \ frac{log_5x^4-2-3(log_5x+ frac{1}{3} )}{log_5x+ frac{1}{3} } textless 0 \ \ frac{4log_5x-2-3log_5x- 1}{log_5x+ frac{1}{3} } textless 0 \ \ frac{log_5x-3}{log_5x+ frac{1}{3} } textless 0$
Точка, в которой числитель меняет знак 
log₅x-3≠0 ⇒  log₅x≠3  ⇒  x≠5³  ⇒  x≠125
Точка, в которой знаменатель меняет знак
log₅x+1/3≠0  ⇒  log₅x≠-1/3   ⇒  $x neq 5^{ -1/3 }$  ⇒ $x neq frac{1}{ sqrt[3]{5} }$

$frac{log_5x-3}{log_5x+ frac{1}{3} } textless 0$     x∈$(frac{1}{ sqrt[3]{5} };125)$
Полученный интервал удовлетворяет   ОДЗ: x>0  

Ответ:  x∈$(frac{1}{ sqrt[3]{5} };125)$