Question

ПОМОГИТЕ ,ПОЖАЛУЙСТА

СРОЧНООО
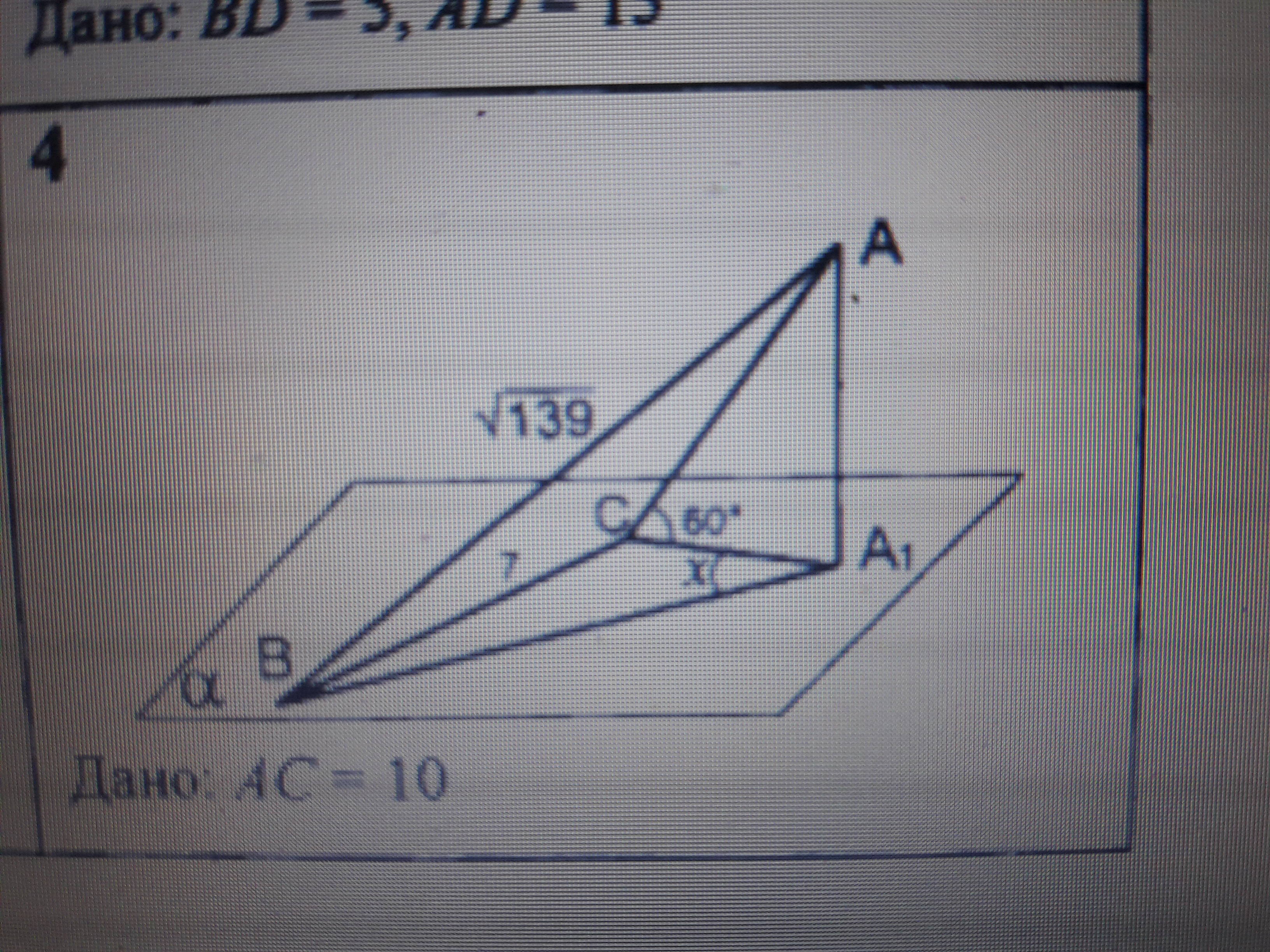
АА1-перпендикуляр к плоскости альфа ,ВЫ и АС -наклонные .Найти х и у .АС=10

Answer 1

Из вершины А треугольника ABC, сторона ВС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр AA1. Найти угол х между СА1 и ВА1,  если АВ =√139 см, ВС=7, AC=10 и угол АСА1=60°
------
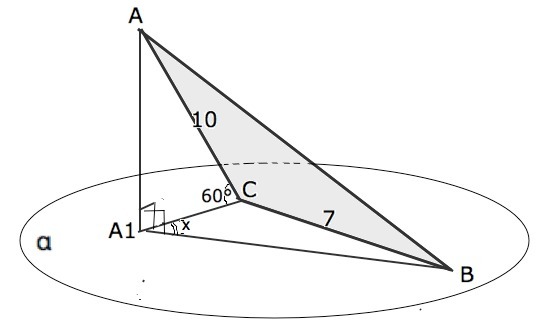
Первое решение верное. Но есть и другой способ нахождения искомого угла, который подтверждает правильность первого. 
Вариант решения. (рисунок вложения  данный в другом ракурсе, на ответ не влияет)

АА1 - перпендикулярен плоскости α, значит, перпендикулярен А1В и А1С.(свойство) 

Из прямоугольного ∆ АА1С катет 

А1С=АС•cos60°=10•1/2=5

катет АА1=АС•sin60°=10•√3/2=5√3

Из прямоугольного ∆ АА1В по т.Пифагора 

А1В=√(AB²-A1B²)=√(139-75)=8

Найдем площадь ∆ ВСА1 по формуле Герона. 

Полупериметр ∆ ВСА1=(5+7+8):2=10 

S (BCA1)=√[(10•(10-8)•(10-7)•(10-5)]=√(5•2•2•3•5)=10√3 

По другой формуле:

S (BCA1)=0,5•A1B•A1C•sinx ⇒

10√3=0,5•8•5•sinx⇒

sinx=20√3:40=√3/2 - это синус 60°

х=60°

Answer 2

Пожалуйста ,помогите с этой задачей ,прошу ,если не сложно https://znanija.com/task/27958905