Question

Найдите диагонали параллелограмма, построенного на векторах а=5р+2q и b=p-3q, если |р|=2√2, |q|=3(над p и q значки векторов). Угол между векторами р и q равен 45°.

Answer 1

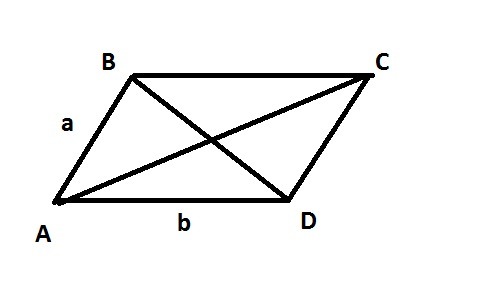
AC=a+b=5p+2q+p-3q=6p-q
|AC|=√((6p)^2+q^2-2*6p*q*cos45)=√(288+9-2*6*2√2*3*√2/2)=√225=15
BD=b-a=p-3q-5p-2q=-4p-5q
|BD|=√(-4p)^2+(-5q)^2-2(-4p)(-5q)cos45)=√593=23.4 примерно...

Answer 2

Где |АС|-это теорема косинусов?

Answer 3

да и где BD -то же

Answer 4

Спасибо)