Question

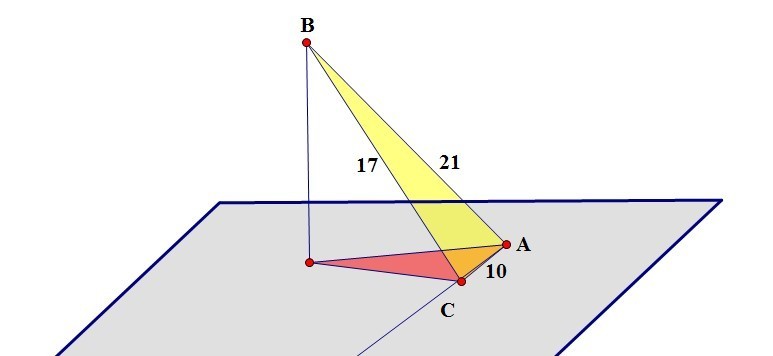
Дано: ∆ABC, AB=21, AC=10, BC=17, AC принадлежит α. Двугранный угол BACO равен 60°, AOC — проекция треугольника ABC на плоскость α. , Найдите площадь ∆AОC. (рисунок пож-та)

Answer 1

Надо вспомнить:
Площадь ортогональной проекции равна площади проектируемой фигуры умноженной на косинус угла между плоскостью многоугольника и плоскостью проекции.
В нашем случае:
ΔАВС - проектируемый треугольник
Δ АОС - проекция треугольника АВС
угол ВАСО - угол между плоскостями

S(AOC)=S(ABC)·cos60°
Осталось найти площадь треугольника АВС. Это можно сделать при помощи формулы Герона. 
S=√(p(p-a)(p-b)(p-c)=84

S(AOC)=84·0,5=42

Answer 2

Решение на фотографии в приложении