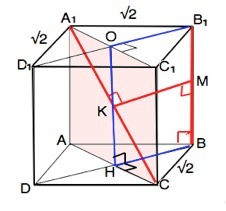
Дано куб с ребром √2 см. Постройте общий перпендикуляр к прямым А1С и ВВ1 и найдите расстояние между этими прямыми.
Ответы
А1С и В1В не параллельны, не пересекаются и не лежат в одной плоскости. А1С и В1В - скрещивающиеся прямые.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
А1С лежит в плоскости А1С1СА.
А1А и В1В параллельны. ⇒ плоскость А1С1СА и прямая В1В параллельны.
Общим перпендикуляром будет отрезок КМ, лежащий в плоскости, проходящей параллельно основаниям куба, т.е. перпендикулярно ВВ1 и плоскости А1С1СА, а, значит, и прямой А1С..
Так как все точки прямой, параллельной плоскости, находятся на одинаковом расстоянии от этой плоскости, искомое расстояние - КМ=ВН=В1О
ABCD - квадрат.
Диагонали квадрата пересекаются под прямым углом и точкой пересечения делятся пополам.
∆ ВНС равнобедренный прямоугольный. Его острые углы равны 45°
ВН=ВС•sin45°=√2•√2:2=1 см.