Question

Из точки А, лежащей на ребре двугранного угла, проведено в разных гранях два перпендикуляра АC и АB до ребра двугранного угла. Найдите градусную меру двугранного угла, если АC = 4√2см, АB= 7, BC = 5см ПОЭТАПНОЕ РЕШЕНИЕ 30 БАЛОВ

Answer 1

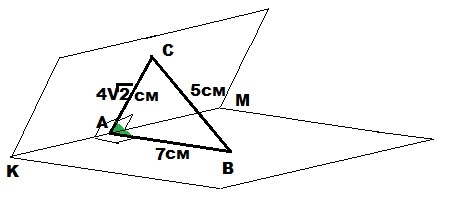
Пусть KM - ребро двугранного угла.
CA⊥KM  и  BA⊥KM   ⇒   
∠CAB = градусной мере двугранного угла

ΔCAB : теорема косинусов
BC² = AC² + AB² - 2AC*AB*cos∠CAB
5² = (4√2)² + 7² - 2 (4√2)*7*cos∠CAB
25 = 32 + 49 - 56√2cos∠CAB
56√2cos∠CAB = 56
cos∠CAB = 1/√2 = √2/2   - табличное значение  cos45°

Ответ: двугранный угол равен 45°