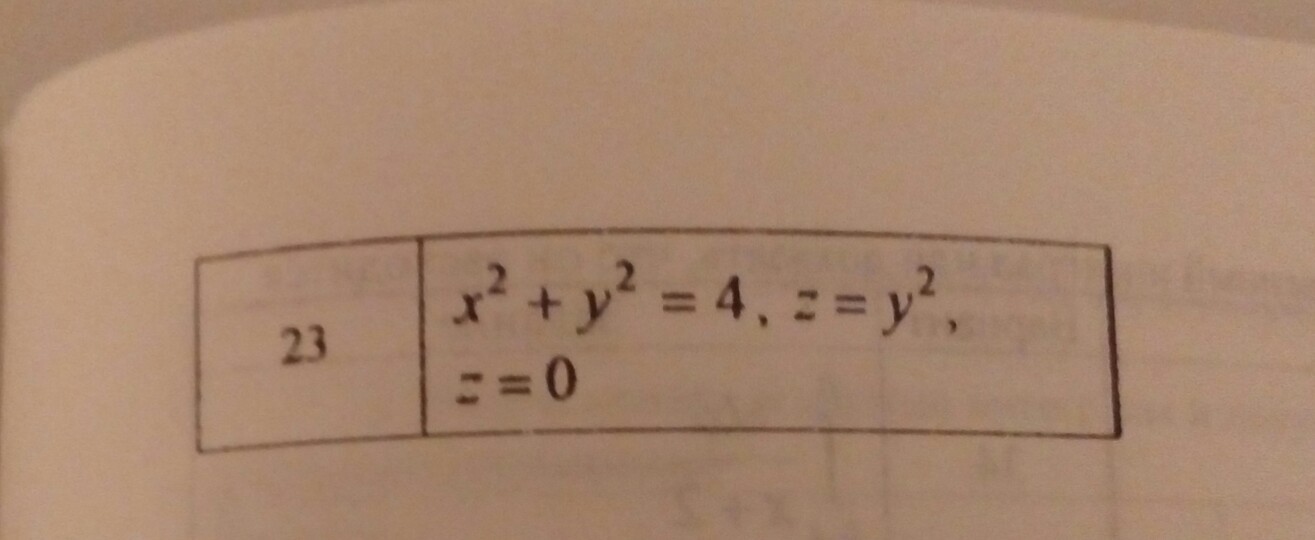Ответы
Ответ дал:
0
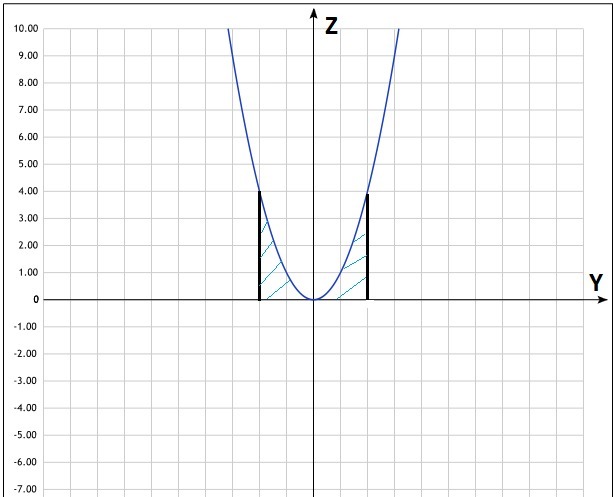
вот в разрезе фигура
Можно найти объем цилиндра, основание круг с радиусом 2(в плоскости ХОУ) и высотой 4
V=4pi*4=16pi
Из него вычитается объем фигуры, образованной вращением ветви параболы вокруг оси z
z=y^2; y=√z
V1=pi*∫(√z)^2dz=pi∫zdz=pi*z^2/2
пределы интегрирования по z от 0 до 4
v1=pi(2-0)=2pi
Тогда объем фигуры. заданной в вопросе будет
V2=V-V1=16pi-2pi=12pi
Можно найти объем цилиндра, основание круг с радиусом 2(в плоскости ХОУ) и высотой 4
V=4pi*4=16pi
Из него вычитается объем фигуры, образованной вращением ветви параболы вокруг оси z
z=y^2; y=√z
V1=pi*∫(√z)^2dz=pi∫zdz=pi*z^2/2
пределы интегрирования по z от 0 до 4
v1=pi(2-0)=2pi
Тогда объем фигуры. заданной в вопросе будет
V2=V-V1=16pi-2pi=12pi
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад