Даю 30 баллов: Найти производную данных функций:
1. y= квадратный корень из arcctg(x/2)
2. y= ln квадратный корень (1+x^2)/(1-x^2)
3. y= ln x^ (1/x)
Данные функции представлены на фото ниже
Приложения:
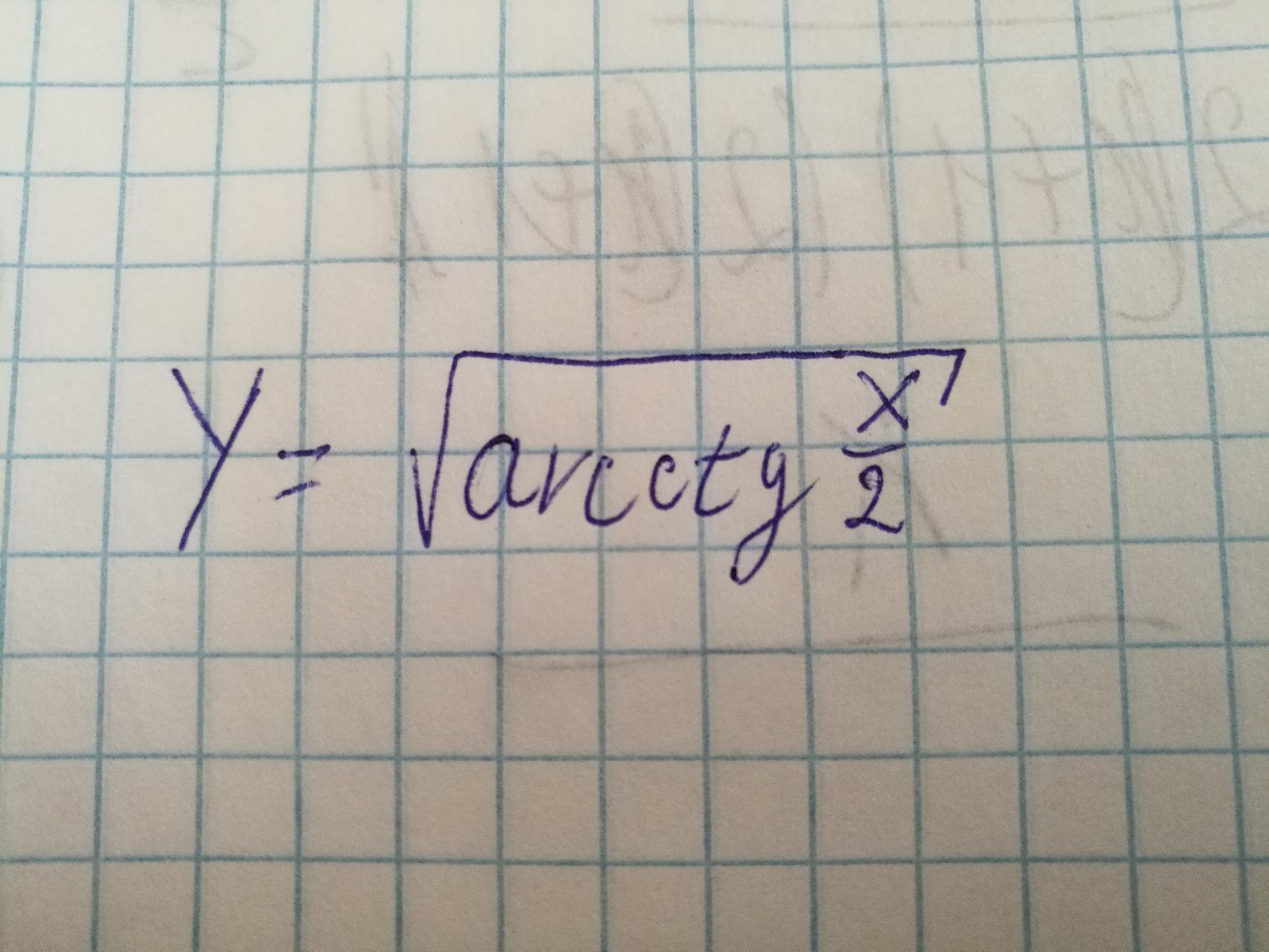
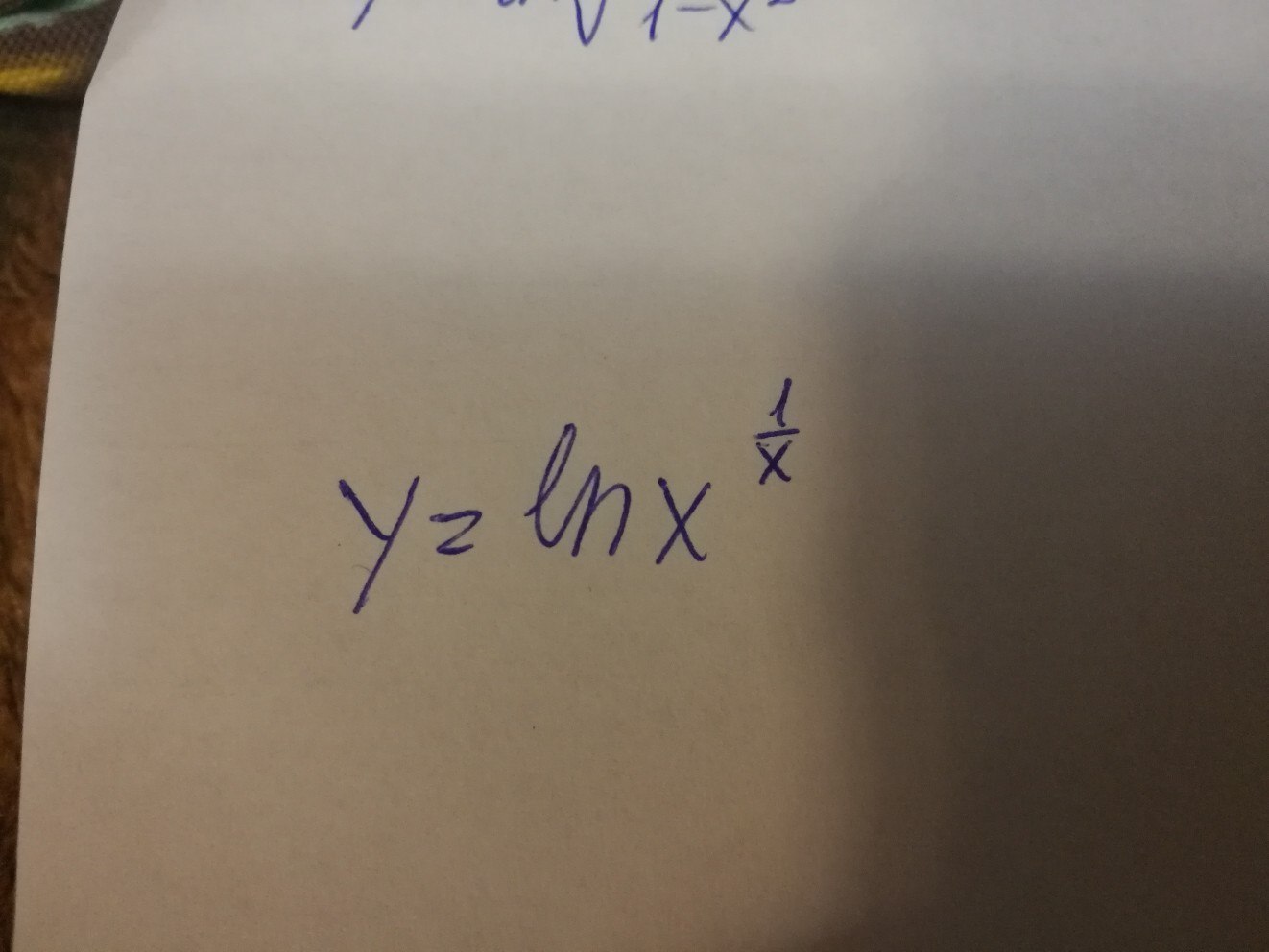
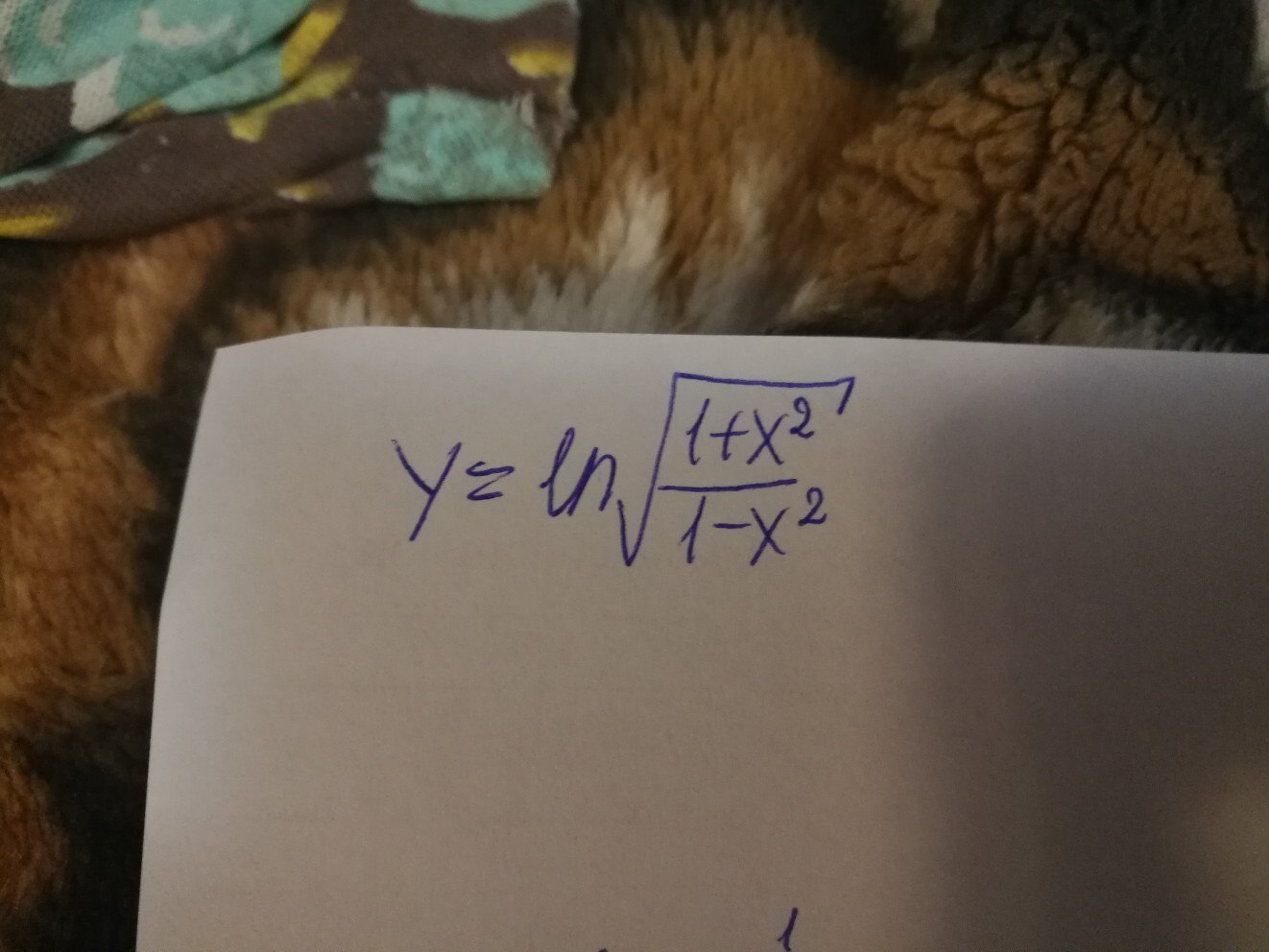
Ответы
Ответ дал:
0
2)
3)
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад