Question

В трапеции ABCD с боковыми сторонами AB и CD угол BAD равен 30° Найдите угол CDA если известно что он является тупым AB=12 и CD=√72. Ответ дайте в градусах.

Answer 1

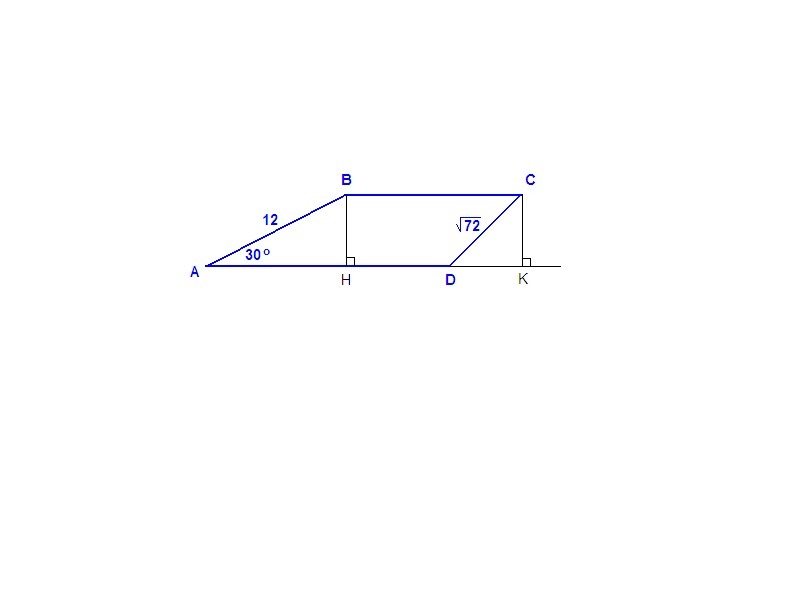
Проведем высоты трапеции ВН и СК.

ΔАВН: ∠АНВ = 90°, ∠ВАН = 30°, АВ = 12, ⇒

ВН = АВ/2 = 6 как катет, лежащий напротив угла в 30°.

СК = ВН = 6 как расстояния между параллельными прямыми.

ΔCKD: ∠CKD = 90°,

sin∠CDK = CK/CD = 6/√72 = 6/(6√2) = 1/√2 = √2/2

Так как по условию угол CDA тупой, то угол CDK, смежный с ним, острый.

∠CDK = 45°.

∠CDA = 180° - ∠CDK = 180° - 45° = 135°