Sn=b1(q^n-1)/q-1 формула (геометрическая прогрессия)
Кто может решить правильно данный пример?
Приложения:

Ответы
Ответ дал:
0
Там по формуле вроде 54 умножить на все выражение, ане только на дробь с степени(см фото), так что вроде так

Приложения:
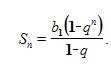
Ответ дал:
0
ой, там даже 1-q, а не q-1 как у тебя, странно
Ответ дал:
0
S=54((2/3)6-1)/(2/3-1)=54*(-3)(64/3^6-1)=
(-2)*3^4(64-3^6)/3^6=(-2)(64-729)/3^2=
2*665/9=1330/9=147 7/9
(-2)*3^4(64-3^6)/3^6=(-2)(64-729)/3^2=
2*665/9=1330/9=147 7/9
Приложения:
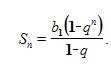
Ответ дал:
0
(-2)*3^4(64-3^6)/3^6 не понимаю почему там знак минус 64-3^6 и в знаменателе тоже 3^6, откуда взялся и куда сократился 3^4 в числителе
Ответ дал:
0
3^4:3^6=3^4:(3^4•3^2)=1/3^2
Ответ дал:
0
2/3-1=(2-3)/3=-1/3
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад