Question

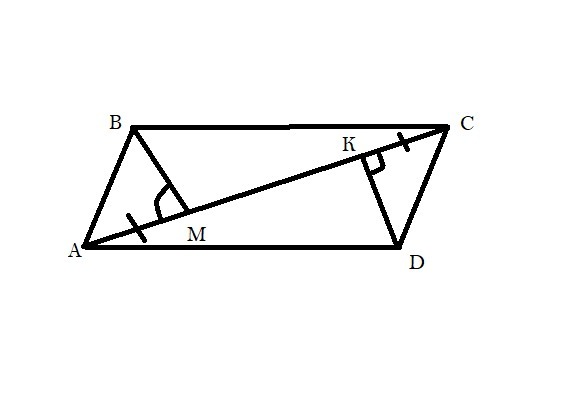
Известно, что AB∥CD, AM=CK, ∠AMB=∠CKD. Докажите, что BC∥AD
Желательно с объяснением, скоро контрольная
(рисунок накидал на Paint, могут быть маленькие неточности)

Answer 1

1) BC || AD => угол АСD  равен углу САВ
2) угол ACD = углу CAB
угол AMB = углу CKD
AM=KC 
Из этого всего следует, что треугольник KCD равен треугольнику BAM
3)Рассмотрим треугольники BMC и AKD
KD=BM(Из 2)
угол AKD = углу BMC(Из 2)
AK=MC(MK - общая часть, AM = KC. AK=AM+MK; MC=MK+KC. Из этого всего следует, что AK=MC)
Из всего третьего пункта следует, что треугольники BMC и AKD равны.
4)Угол DAC = углу BCA. Они накрест лежащие. Из этого следует, что AD=BC.
Ч.т.д.

Answer 2

Вроде бы понял

Answer 3

AD||BC да?