Question

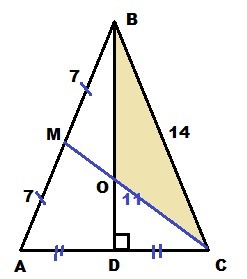
.Треугольник АВС равнобедренный, АВ = ВС = 14, медиана СМ
равна 11. Высота ВD пересекает медиану СМ в точке О. Найти площадь
треугольника BOС.

Answer 1

CM - медиана  ⇒  AM = MB = 14/2 = 7
Площадь  ΔCMB  по формуле Герона
$p = frac{14+11+7}{2} =16 \ \ S_{CMB}= sqrt{p(p-a)(p-b)(p-c)} = \ \ = sqrt{16(16-14)(16-11)(16-7)} = \ \ = sqrt{16*2*5*9} = 12 sqrt{10}$
Медиана CM делит ΔABC на два равновеликих.
Высота BD также и медиана в равнобедренном треугольнике, тоже делит ΔABC на два равновеликих ⇒
$S_{CBD}=S_{CMB}=12 sqrt{10}$
Медианы BD и CM точкой пересечения O делятся в отношении 2:1 от вершины     ⇒ BO:OD = 2:1  ⇒  OB = 2/3 BD
$S_{BOC}= frac{ BO*CD}{2} = frac{ frac{2}{3}BD*CD }{2} = \ \ =frac{2}{3} *( frac{BD*CD}{2} )= frac{2}{3} S_{CBD}= frac{2}{3} *12 sqrt{10} =8 sqrt{10}$

Ответ: площадь ΔBOC    S=8√10