Ответы
Ответ дал:
0
ДАНО
Y = 18 + 3*x - x²
Y = 0
НАЙТИ
S = ? - площадь.
РЕШЕНИЕ
Находим пределы интегрирования - решаем квадратное уравнение.
a = 6, b = -3.
Находим интеграл разности функций (вторая = 0)

Вычисляем подставив пределы интегрирования.
S(6) = 108+54-72 = 90
S(-3)) = -54 +13.5 + 9 = - 31.5
S = 90 - (-31.5) = 121.5 - площадь - ОТВЕТ
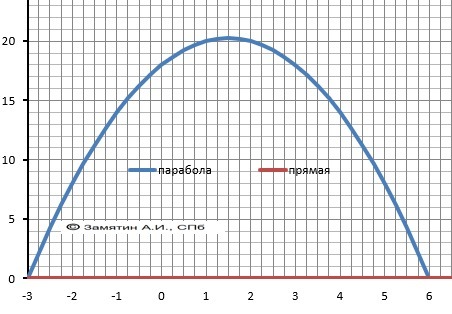
Рисунок к задаче в приложении.
Y = 18 + 3*x - x²
Y = 0
НАЙТИ
S = ? - площадь.
РЕШЕНИЕ
Находим пределы интегрирования - решаем квадратное уравнение.
a = 6, b = -3.
Находим интеграл разности функций (вторая = 0)
Вычисляем подставив пределы интегрирования.
S(6) = 108+54-72 = 90
S(-3)) = -54 +13.5 + 9 = - 31.5
S = 90 - (-31.5) = 121.5 - площадь - ОТВЕТ
Рисунок к задаче в приложении.
Приложения:
Ответ дал:
0
Ответ:
S = 121.5
Объяснение:
Найдём точки пересечения параболы у = -х² + 3х + 18 с осью. Ох, заданной уравнением у = 0.
Решаем уравнение -х² + 3х + 18 = 0
D = 9 + 72 =81
√D = 9
x₁ = (-3 - 9)/(-2) = 6
x₂ = (-3 + 9)/(-2) = -3
Найдём координаты вершины параболы (m; n)
m = -3 : (-2) = 1.5; n = y(m) = -2.25 + 3 · 1.5 + 18 = 20.25
и точку её пересечения с осью Оу: у(0) = 18
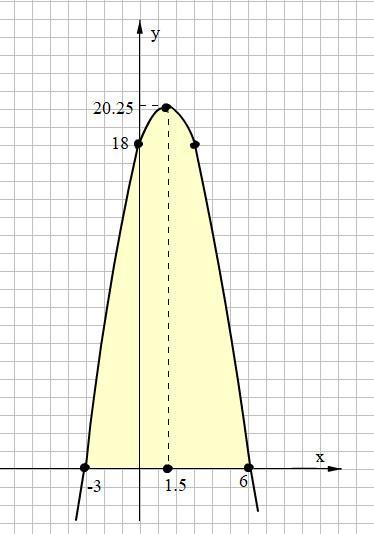
Построим параболу (смотри рисунок на прикреплённом фото).
Площадь фигуры, ограниченной параболой и осью Oх закрашена.
Найдём эту площадь.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад