Question

отрезки AB и CM параллельны и равны. докажите, что AM=BC.

Answer 1

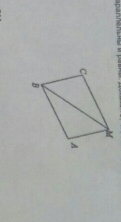
угол AMB равен углу MBC как накрест лежащие при пересечении двух параллельных прямых AB и CM секущей MB
Аналогично, угол CMB равен углу AMB
BM - общая сторона двух треугольников BCM и BAM
Следовательно, треугольник BCM равен треугольнику BAM по стороне и двум прилежащим углам -> AM = BC , что и требовалось доказать

Answer 2

Рассмотрим треугольники ВМС и АВМ
∠ВМС=∠МВА как накрест лежащие при параллельных прямых СМ , АВ и секущей ВМ; СМ=АВ по условию;ВМ-общая⇒ΔВМС=ΔАВМ по первому признаку⇒АМ=ВС,т.к. находятся в равных треугольниках напротив равных углов