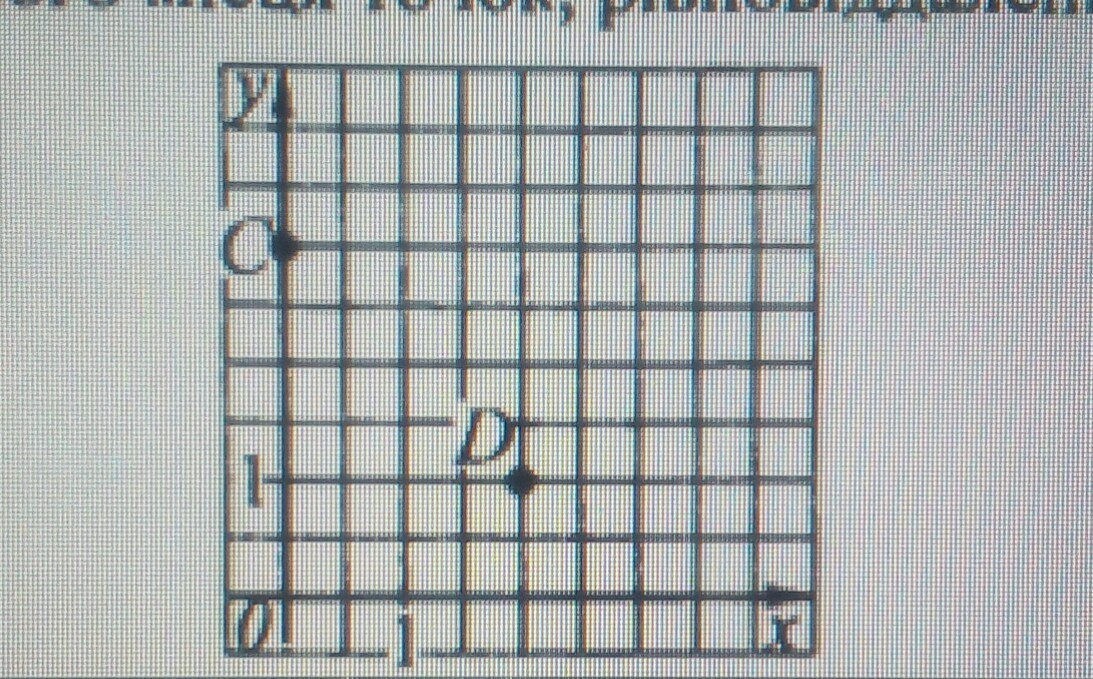
45 баллов. Составить уравнение геометрического места точек, равноотдалённых от точек С (0;3) и D (2;1). (см. рисунок)
P.S. варианты ответов: а) у=х+3, б) у=х+1, в) у=х+2, г) у=(-х)+1 д) у=2
P.P.S. С подробным (!) решением!
Приложения:
Ответы
Ответ дал:
1
ГМТ(геометрическое место точек) равноудаленных от концов отрезка является серединным перпендикуляром этого отрезка. Отсюда это прямая, проходит через тК((0+2)/2;(3+1)/2) К(1;2) где К - середина СД. Чтобы определить уравнение искомой прямой, нам нужно уравнение прямой СД, так как искомая прямая перпендикулярна СД. Пусть уравнение СД :y=kx+b
СД проходит через точки (0,3) (2,1) отсюда имеем систему: 3=b и 2k+b=1.Решив её получаем b=3, k=-1 отсюда уравнение прямой СД:y=-x+3. Так как искомая прямая перпендикулярна прямой СД, то если она имеет уравнение y=k1x+b1, то k1=1 Отсюда прямая, перпендикулярная СД будет иметь вид y=x+b. Также эта прямая проходит через тК(1;2) отсюда 2=1+k, к=1. Тогда уравнение искомой прямой y=x+1
СД проходит через точки (0,3) (2,1) отсюда имеем систему: 3=b и 2k+b=1.Решив её получаем b=3, k=-1 отсюда уравнение прямой СД:y=-x+3. Так как искомая прямая перпендикулярна прямой СД, то если она имеет уравнение y=k1x+b1, то k1=1 Отсюда прямая, перпендикулярная СД будет иметь вид y=x+b. Также эта прямая проходит через тК(1;2) отсюда 2=1+k, к=1. Тогда уравнение искомой прямой y=x+1
Аноним:
Можно было чуть схалтурить, и сказать что точка (0;1) также равноудалена от сторон отрезка СД, предоставив док-во. Ну и тогда сказать, что искомая прямая проходит через тК и через (0;1) и найти уравнение прямой чуть проще
Спасибо большое!
Аа, как отменить поставленную собой же оценку, я вкладки перепутал)
Если не ошибаюсь, здесь нет такой функции, — но это ведь ничего страшного) пускай будет:)
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
8 лет назад