Question

100 БАЛЛОВ!
Биссектриса CL треугольника ABC делит сторону AB на отрезки AL=11 и BL=9.
Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите длину отрезка CD.

Answer 1

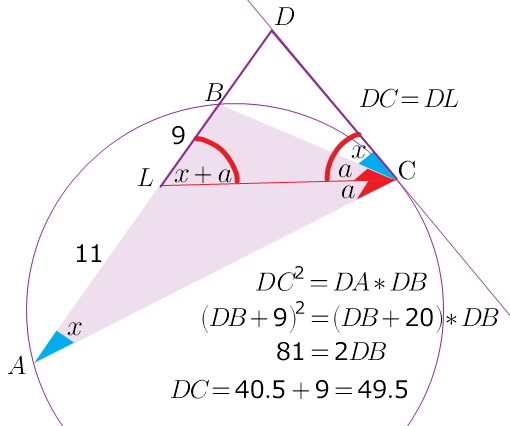
1 теорема: Квадрат длины касательной (DC) = произведению длины                               секущей (DA), проведенной из той же точки (у нас это D),
                   на ее внешнюю часть (DB). 
2 теорема: Угол между касательной (DC) и хордой (BC), проведенными из                     одной точки (у нас это С), = половине градусной меры дуги,
                   заключенной между касательной и хордой.
и вписанный угол ВАС = половине градусной меры той же дуги...
легко заметить, что треугольник DLC окажется равнобедренным))