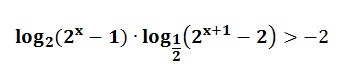Ответы
Ответ дал:
0
1) разбираемся со 2-м логарифмом: приведём его к основанию = 2
log₁/₂(2ˣ⁺¹ -2) = log₂(2ˣ⁺¹ -2)/log₂(1/2) = -log₂(2ˣ⁺¹ -2) = -log₂(2(2ˣ -1)) =
= - log₂2 - log₂(2ˣ -1)
сам пример: log₂(2ˣ -1)*(- log₂2 - log₂(2ˣ -1))> -2
log₂(2ˣ -1)*(1 + log₂(2ˣ -1)) < 2
Сначала ОДЗ: 2ˣ -1 > 0, ⇒2ˣ > 1, ⇒ x > 0
2) теперь решаем:
log₂(2ˣ -1) = t
t(1 +t) < 2
t +t² -2 < 2
t² +t -2 < 0
по т. Виета корни -2 и 1
решение : -2 < t < 1
-2< log₂(2ˣ -1) < 1
log₂(1/4) < log₂(2ˣ -1) < log₂2
1/4 < 2ˣ -1 < 2
5/4 < 2ˣ < 3
2^log₂(5/4) < 2ˣ < 2^log₂3
log₂(5/4) < x < log₂3
log₁/₂(2ˣ⁺¹ -2) = log₂(2ˣ⁺¹ -2)/log₂(1/2) = -log₂(2ˣ⁺¹ -2) = -log₂(2(2ˣ -1)) =
= - log₂2 - log₂(2ˣ -1)
сам пример: log₂(2ˣ -1)*(- log₂2 - log₂(2ˣ -1))> -2
log₂(2ˣ -1)*(1 + log₂(2ˣ -1)) < 2
Сначала ОДЗ: 2ˣ -1 > 0, ⇒2ˣ > 1, ⇒ x > 0
2) теперь решаем:
log₂(2ˣ -1) = t
t(1 +t) < 2
t +t² -2 < 2
t² +t -2 < 0
по т. Виета корни -2 и 1
решение : -2 < t < 1
-2< log₂(2ˣ -1) < 1
log₂(1/4) < log₂(2ˣ -1) < log₂2
1/4 < 2ˣ -1 < 2
5/4 < 2ˣ < 3
2^log₂(5/4) < 2ˣ < 2^log₂3
log₂(5/4) < x < log₂3
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад