В прямоугольном треугольнике АВС угол В равен 90 градусов, точка N – середина стороны ВС, точка М- середина стороны АВ. Угол NМВ равен 60 градусов, NМ =12см. Найти стороны треугольника АВС и площадь треугольника В NМ. помогите
Ответы
Ответ дал:
0
MN - средняя линия треугольника АВС
MN=12 ⇒ AC=24
∠BMN=60°⇒∠MNB=30°
MB=6 - катет против угла в 30° равен половине гипотенузы
AB=12
По теореме Пифагора
BC=√(24²-12²)=12√(3)
BN=6√(3)
S(ΔBMN)=(1/2)MB·BN=(1/2)·6·6√3=18√3 кв. см
MN=12 ⇒ AC=24
∠BMN=60°⇒∠MNB=30°
MB=6 - катет против угла в 30° равен половине гипотенузы
AB=12
По теореме Пифагора
BC=√(24²-12²)=12√(3)
BN=6√(3)
S(ΔBMN)=(1/2)MB·BN=(1/2)·6·6√3=18√3 кв. см
Приложения:
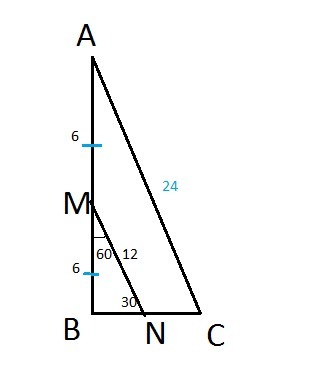
Ответ дал:
0
cgfcb,j
Ответ дал:
0
спаисбо
Ответ дал:
0
спасибо
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад