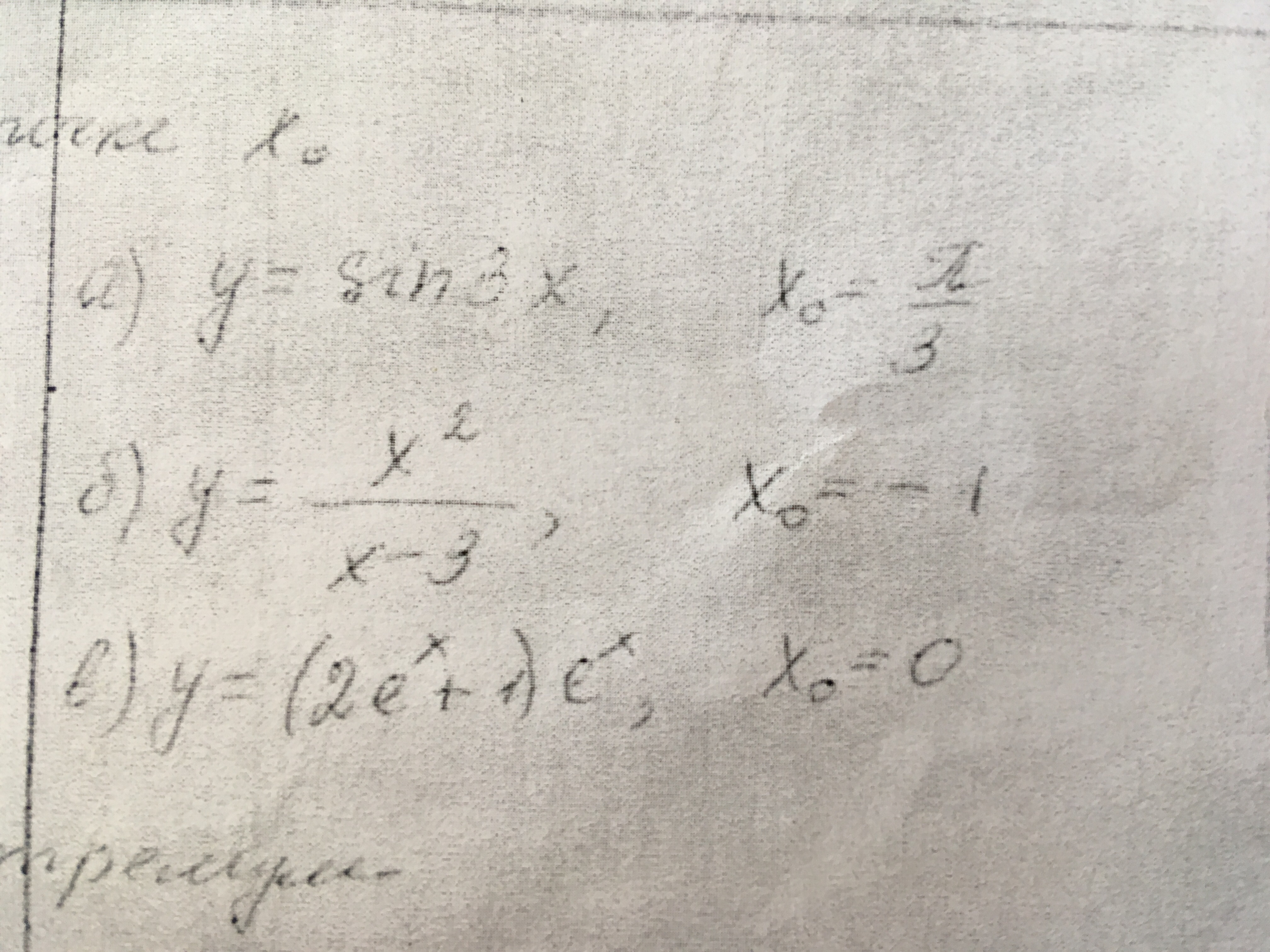Ответы
Ответ дал:
0
y=sin(3x)
y'=(sin(3x))'=3cos(3x)
y'(π/3)=3cos(3*π/3)=3cosπ=3



y'=(sin(3x))'=3cos(3x)
y'(π/3)=3cos(3*π/3)=3cosπ=3
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад