Question

ОТДАЮ ВСЕ БАЛЛЫ!!! НУЖНА ПОМОЩЬ!!! ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ
подозреваю что через замену, но не пойму как...

Answer 1

Решение прикреплено.

Answer 2

почему нет проверки на ОДЗ?

Answer 3

Потому что при решении простейших уравнений вида logx=a ОДЗ не расширяется, и посторонних корней появиться не может. В таких уравнениях проверка по ОДЗ излишняя. А корень второго уравнения был проверен непосредственной подстановкой.

Answer 4

$log_{2} ^{2} x+(x-1) log_{2} x=6-2x \ \ ODZ: x textgreater 0 \ \ log_{2} ^{2} x+(x-1) log_{2} x-6+2x =0 \ \ D=(x-1)^2-4(2x-6)=x^2-2x+1-8x+24=(x-5)^2 \ \ 1) log_{2} x=(-x+1+x-5)/2=-2= log_{2} 2^{-2} =log_{2} frac{1}{4} \ \ x= frac{1}{4} \ \ 2)log_{2} x=(-x+1-x+5)/2=-x+3$

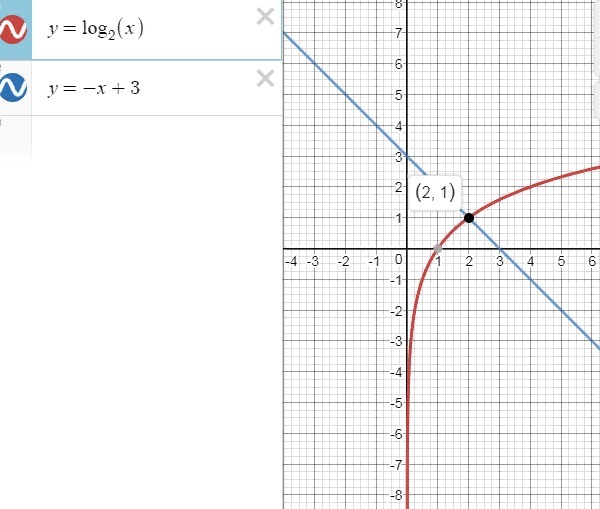
слева функция возрастает , справа убывает  ⇒ корень один х=2
находится подбором или графически

ОТВЕТ : {0.25;2}