Question

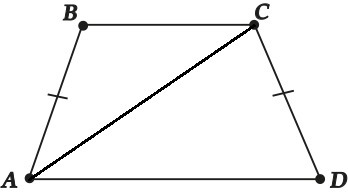
в равнобедренной трапеции abcd основание ad равно 20 см.Периметр трапеции равен 47 см ,диагональ AC является биссектрисой угла A .Найдите боковые стороны трапеции

Answer 1

Вот решение:

∠BAC = ∠CAD т.к. AC - биссектриса.

∠BCA = ∠CAD т.к. данный углы накрест лежащие при параллельных прямых.

⇒ ∠BAC = ∠CAD ⇒ ΔABC - равнобедренный.

⇒ AB = BC = СD (AB = CD т.к. трапеция равнобедренная)

Пусть AB = BC = СD = x.

Тогда 3х + 20 = 47
3х = 27
х = 9

Ответ: AB = CD = 9

Answer 2

pravilno

Answer 3

sps