Исследовать сходимость , абсолютную сходимость и расходимость.
ДАЮ 100 БАЛЛОВ! СРОЧНА!!!
Приложения:
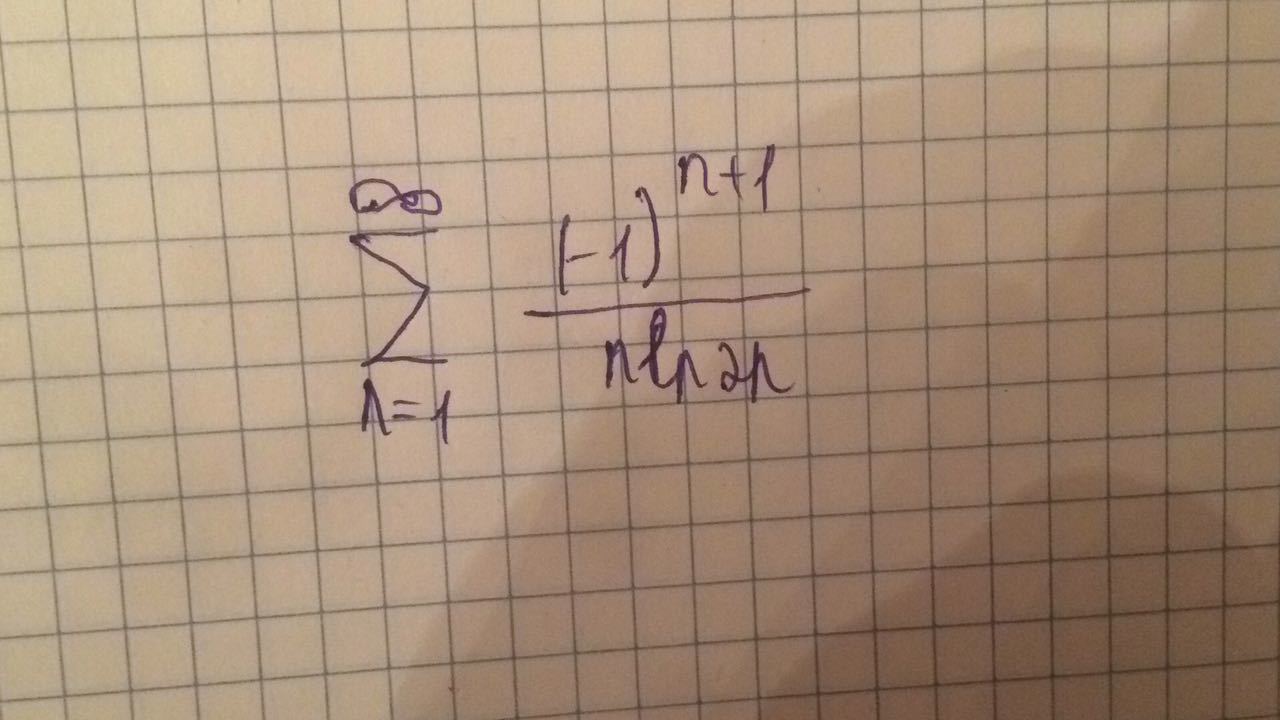
Ответы
Ответ дал:
0
Первое условие признака Лейбница выполняется 1/ln2 > 1/ln8 > 1/ln216
 Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится.
Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится.
Исследуем теперь ряд на абсолютность. Возьмём ряд по модулю
 Применим интегральный признак:
Применим интегральный признак:
 Несобственный интеграл расходится, следовательно и ряд по модулю тоже расходится, а значит данный ряд будет сходится УСЛОВНО
Несобственный интеграл расходится, следовательно и ряд по модулю тоже расходится, а значит данный ряд будет сходится УСЛОВНО
Исследуем теперь ряд на абсолютность. Возьмём ряд по модулю
Ответ дал:
0
https://znanija.com/task/28419645
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад