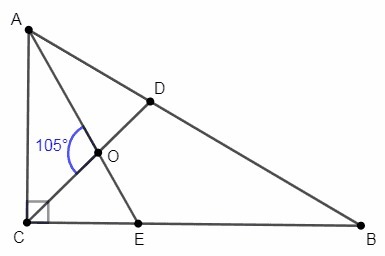
В прямоугольном треугольнике ABC (угол C=90гр.) биссектрисы CD и AE пересекаются в точке O. угол AOC=105гр. Найдите острые углы треугольника ABC
ПОЖАЛУЙСТА РЕБЯТА!!!
Ответы
Ответ дал:
0
∠C=90°, ∠AOC=105°
Биссектриса делит угол пополам.
∠CAO=∠A/2
∠ACO=∠C/2 =90°/2 =45°
Сумма углов треугольника 180°.
∠CAO+∠AOC+∠ACO=180° <=>
∠A/2 +105° +45° =180° <=>
∠A= 2(180°-105°-45°) =60°
Сумма острых углов прямоугольного треугольника 90°.
∠B= 90°-∠A =90°-60° =30°
Биссектриса делит угол пополам.
∠CAO=∠A/2
∠ACO=∠C/2 =90°/2 =45°
Сумма углов треугольника 180°.
∠CAO+∠AOC+∠ACO=180° <=>
∠A/2 +105° +45° =180° <=>
∠A= 2(180°-105°-45°) =60°
Сумма острых углов прямоугольного треугольника 90°.
∠B= 90°-∠A =90°-60° =30°
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад