Question

В треугольнике ABC угол C равен 90 градусов, AB = 5, tg A = 3/4. Найдите высоту CH.

Answer 1

Ответ:   2,4

Объяснение:

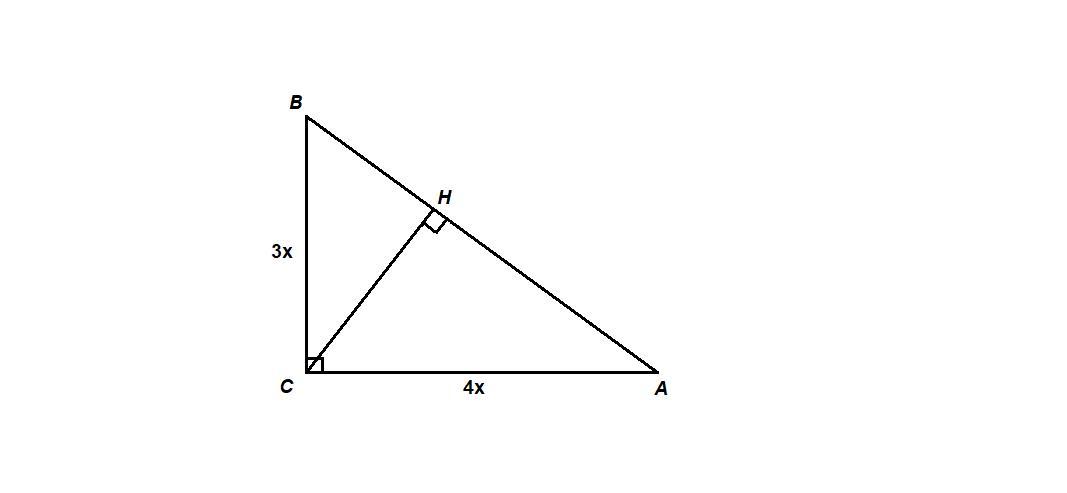
Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему:

tg A = BC / AC = 3/4

Пусть х - коэффициент пропорциональности (x > 0), тогда

ВС = 3х,  АС = 4х.

По теореме Пифагора:

ВС² + АС² = АВ²

(3x)²  + (4x)² = 25

9x² + 16x² = 25

25x² = 25

x² = 1

x = 1  

BC = 3,  AC = 4.

Площадь прямоугольного треугольника:

S = 1/2 BC · AC =  1/2 AB · CH

CH = BC · AC / AB = 3 · 4 / 5 = 2,4