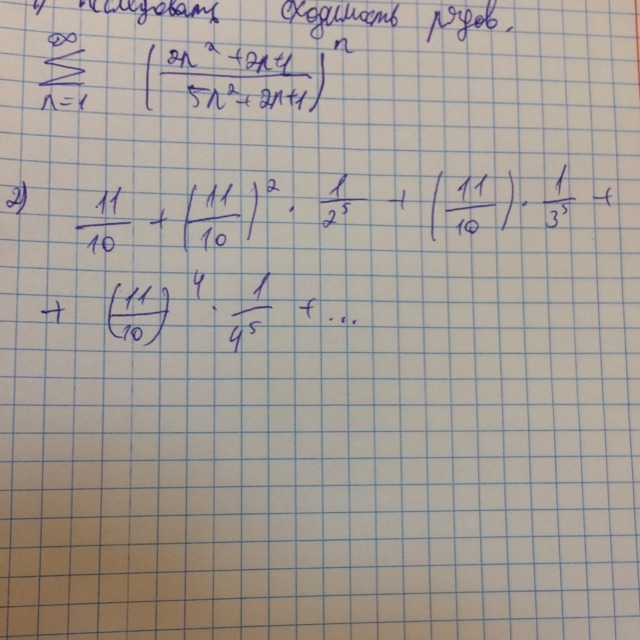Ответы
Ответ дал:
0
общий член ряда

радикальный признак используем:
![lim_{n to infty} sqrt[n]{( frac{10}{11})^{n}* frac{1}{n^{5}}} =
lim_{n to infty} ( frac{10}{11} * frac{1}{ sqrt[n]{n^{5}} } )= frac{10}{11} * lim_{n to infty} frac{1}{ (sqrt[n]{n})^{5} } = \ \ = frac{10}{11} * frac{1}{1^{5}} = frac{10}{11} lim_{n to infty} sqrt[n]{( frac{10}{11})^{n}* frac{1}{n^{5}}} =
lim_{n to infty} ( frac{10}{11} * frac{1}{ sqrt[n]{n^{5}} } )= frac{10}{11} * lim_{n to infty} frac{1}{ (sqrt[n]{n})^{5} } = \ \ = frac{10}{11} * frac{1}{1^{5}} = frac{10}{11}](https://tex.z-dn.net/?f=+lim_%7Bn+to+infty%7D++sqrt%5Bn%5D%7B%28+frac%7B10%7D%7B11%7D%29%5E%7Bn%7D%2A+frac%7B1%7D%7Bn%5E%7B5%7D%7D%7D+%3D%0A+lim_%7Bn+to+infty%7D+%28+frac%7B10%7D%7B11%7D+%2A+frac%7B1%7D%7B+sqrt%5Bn%5D%7Bn%5E%7B5%7D%7D+%7D+%29%3D+frac%7B10%7D%7B11%7D+%2A+lim_%7Bn+to+infty%7D++frac%7B1%7D%7B+%28sqrt%5Bn%5D%7Bn%7D%29%5E%7B5%7D+%7D++%3D+%5C++%5C+%3D+frac%7B10%7D%7B11%7D+%2A+frac%7B1%7D%7B1%5E%7B5%7D%7D+%3D+frac%7B10%7D%7B11%7D+)
10/11<1 ⇒ ряд сходится
радикальный признак используем:
10/11<1 ⇒ ряд сходится
Ответ дал:
0
Остальные реши
Ответ дал:
0
Предел равняется нулю)
Ответ дал:
0
привет Гаутер, я уже раз рассписывал предел (х)^(1/x)=1
Ответ дал:
0
степень быстрее стремится к нулю чем подстепенное..
Ответ дал:
0
ну нет желания еще раз приводить доказательство, тем более в комментариях..
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Приложения:

Ответ дал:
0
У Коши несколько признаков, хочу внести ясность по тому, к которому
применяю решение этого задания.
Пользуюсь радикальным признаком Коши в предельной форме.
Приложения:

Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад