Question

Докажите, что площадь правильного 2n-угольника равна (n*a{n}*R)/2. Где a{n} – сторона многоугольника, R – радиус описанной около него окружности, n – число его сторон.

Answer 1

РЕШЕНИЕ
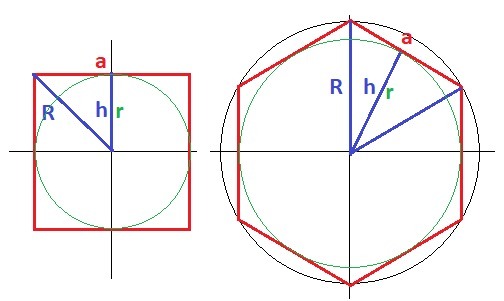
Площадь многоугольника разбивается на сумму площадей треугольников S = n* (a*h/2), где h = r - радиус вписанной окружности. 
Для четырехугольника -  n = 2
S4 = 2*a*(a/2) = a² - площадь квадрата.
В общем виде
S(2n) = p*h/2 = n*a*r/2 - площадь.
В формуле используется радиус вписанной окружности.
Рисунок к задаче в приложении.