Равнобедренный треугольник вращается вокруг основания. Сторона основания равна 10, боковая сторона 13. Найдите площадь поверхности тела вращения, в ответ запишите S/pi.
Ответы
Ответ дал:
0
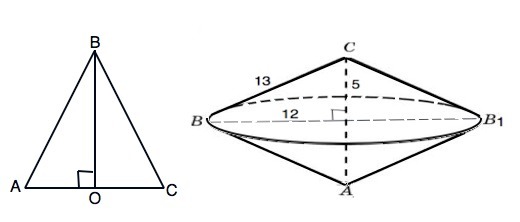
Треугольник АВС с боковыми сторонами 13 и основанием АС=10 вращается вокруг АС как вокруг оси.
При этом получается тело, похожее на "волчок" - два конуса с общим основанием с радиусом, равным высоте ВО треугольника АВС.
В треугольнике АВС высота ВО=√(AB²-AО²)=√(13²-5²)=12
а)
Площадь тела вращения – сумма площадей боковой поверхности двух конусов. Формула боковой поверхности конуса S=πRL
R=12
2•S =π•12•13=312π (ед. площади)
б)
Объем данного тела вращения - сумма объёмов двух равных конусов.
V=πR²•h/3
2V=π•144•5/3=480π (ед. объема)
При этом получается тело, похожее на "волчок" - два конуса с общим основанием с радиусом, равным высоте ВО треугольника АВС.
В треугольнике АВС высота ВО=√(AB²-AО²)=√(13²-5²)=12
а)
Площадь тела вращения – сумма площадей боковой поверхности двух конусов. Формула боковой поверхности конуса S=πRL
R=12
2•S =π•12•13=312π (ед. площади)
б)
Объем данного тела вращения - сумма объёмов двух равных конусов.
V=πR²•h/3
2V=π•144•5/3=480π (ед. объема)
Приложения:
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад