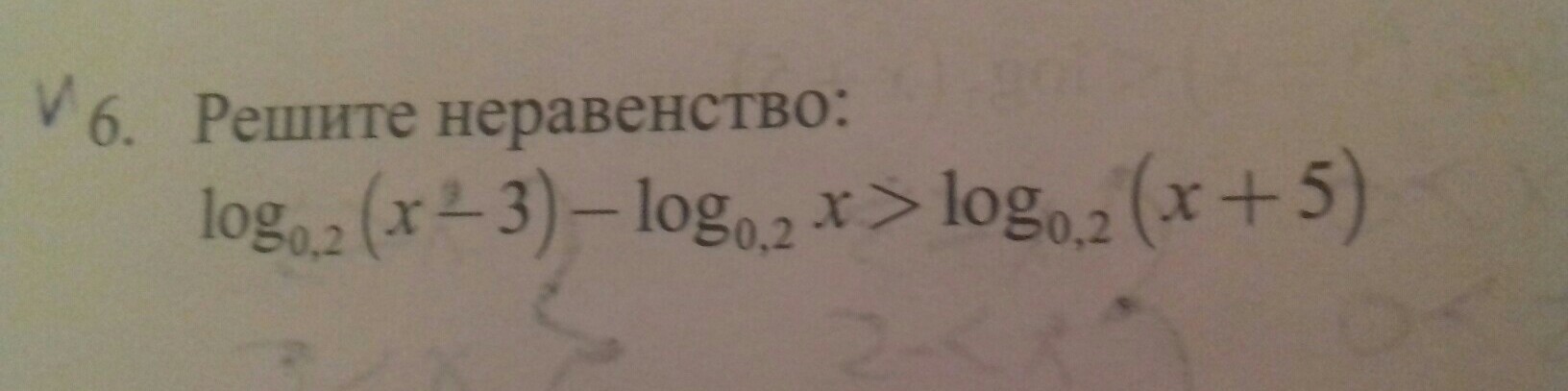Ответы
Ответ дал:
0
одз: x-3>0 x>3
x>0 x>0
x+5>0 x>-5 x∈(3;+∞)
㏒₀,₂(x-3)/x>㏒₀,₂(x+5)
0<0,2<1 (x-3)/x<x+5 т.к. x>0, можем обе части умножить на х, знак неравенства не поменяется
x-3<x²+5x
x²+4x+3>0 x²+4x+3=0 x₁+x₂=-4 x₁x₂=3 x₁=-1 x₂=-3
на промежутке (-∞;-3) x²+4x+3>0
на промежутке (-3;-1) x²+4x+3<0
на промежутке (-1;+∞) x²+4x+3>0 значит х∈(-∞;-3)∪(-1;+∞)
учитывая одз окончательно х∈(3;+∞)
x>0 x>0
x+5>0 x>-5 x∈(3;+∞)
㏒₀,₂(x-3)/x>㏒₀,₂(x+5)
0<0,2<1 (x-3)/x<x+5 т.к. x>0, можем обе части умножить на х, знак неравенства не поменяется
x-3<x²+5x
x²+4x+3>0 x²+4x+3=0 x₁+x₂=-4 x₁x₂=3 x₁=-1 x₂=-3
на промежутке (-∞;-3) x²+4x+3>0
на промежутке (-3;-1) x²+4x+3<0
на промежутке (-1;+∞) x²+4x+3>0 значит х∈(-∞;-3)∪(-1;+∞)
учитывая одз окончательно х∈(3;+∞)
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад