Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж.
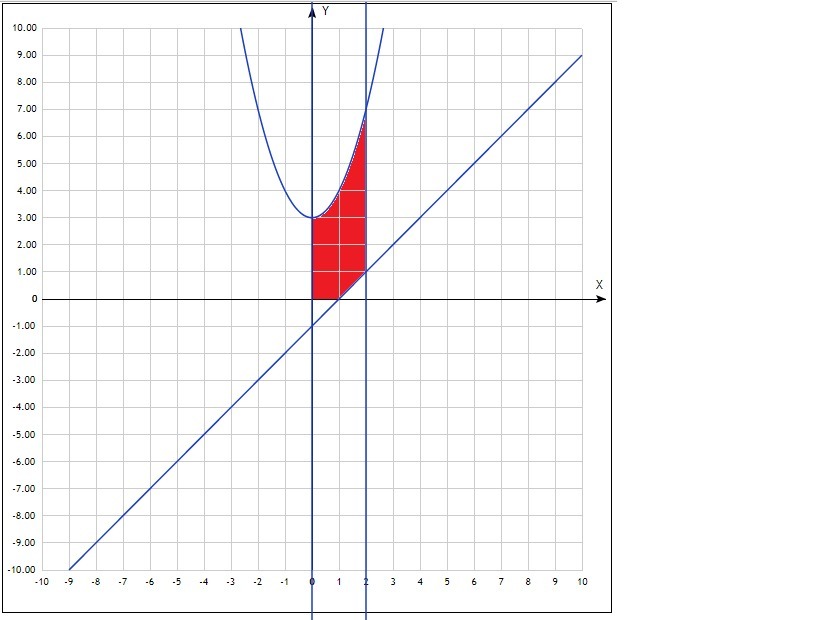
y=x^2+3, x=0, y=x-1, x=2
Ответы
Ответ дал:
0
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад