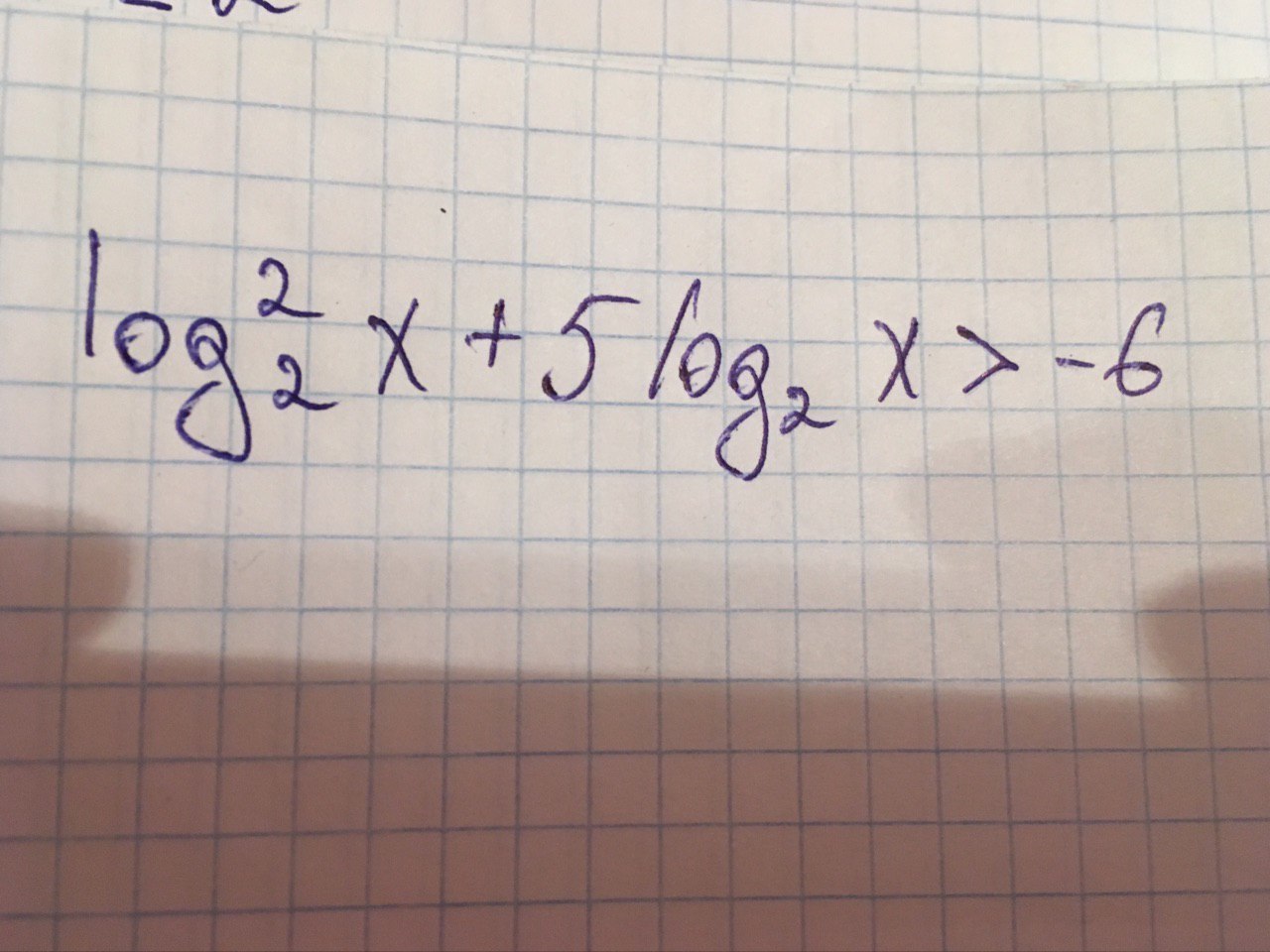Ответы
Ответ дал:
0
log²2 (x) + 5log2 (x)>-6
log²2 (x) + 5log2 (x) +6>0
Пусть log2 (x)=t,тогда:
t²+5t+6>0
t²+5t+6=0
{t₁+t₂=-5,
{t₁*t₂=6.
t₁=-3
t₂=-2
__+_____-3____-____-2___+___t
t∈(-∞;-3)∪(-2;+∞)
Обратная замена:
log2 (x)∈(-∞;-3)∪(-2;+∞)
x∈(0; 2⁻³)∪(2⁻²;+∞)
Ответ:x∈(0;1/8)∪(1/4;+∞)
log²2 (x) + 5log2 (x) +6>0
Пусть log2 (x)=t,тогда:
t²+5t+6>0
t²+5t+6=0
{t₁+t₂=-5,
{t₁*t₂=6.
t₁=-3
t₂=-2
__+_____-3____-____-2___+___t
t∈(-∞;-3)∪(-2;+∞)
Обратная замена:
log2 (x)∈(-∞;-3)∪(-2;+∞)
x∈(0; 2⁻³)∪(2⁻²;+∞)
Ответ:x∈(0;1/8)∪(1/4;+∞)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад