Question

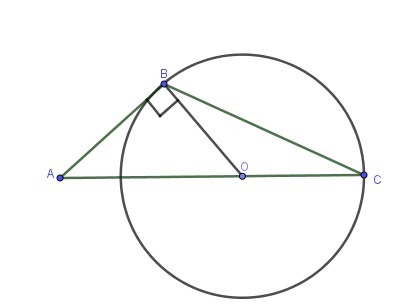
Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АБ в точке Б .Найдите AC,если диаметр окружности равен 7,5, а AB=2

Answer 1

Свойство касательной: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, то есть ВО ⊥ AB.

Диаметр окружности в два раза меньше за радиус, то есть BO=OC=7.5/2=3.75 . Тогда из прямоугольного треугольника ABO:

$AO=sqrt{AB^2+BO^2}=sqrt{2^2+3.75^2} =4.25$

Тогда $AC=AO+OC=4.25+3.75=8$

Ответ: 8.