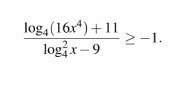Question

log4(16x^4)+11/log^2 4(x)-9≥-1

Answer 1

$frac{ log_{4}(16x^4)+11 }{ log_{4} ^{2}x-9 } geq -1$

одз
{x>0
{x≠64
{x≠1/64

$frac{log_{4} 16+4 log_{4}x+11+ log_{4} ^{2}x-9 }{(log_{4}x-3)(log_{4}x+3)} geq 0 \ \ frac{log_{4} ^{2}x+4log_{4}x+4}{(log_{4}x- log_{4}64 )(log_{4}x- log_{4} frac{1}{64} )} geq 0 \ \ frac{(log_{4}x-log_{4} frac{1}{16} )^2}{(log_{4}x- log_{4}64 )(log_{4}x- log_{4} frac{1}{64} )} geq 0 \ \ frac{(x- frac{1}{16})^2 }{(x-64)(x- frac{1}{64}) } geq 0$

+++++(1/64)-----------[1/16]---------(64)

x∈(-∞;1/64)U{1/16}U(64;+∞)

с учетом одз получаем ответ

x∈(0;1/64)U{1/16}U(64;+∞)

Answer 2

а можете написать из чего следует 64 и 1/64, пожалуйста?

Answer 3

4^3=64;4^(-3)=1/64

Answer 4

спасибо

Answer 5

если заменить на t, одз можео не писать?