Question

Две плоскости, параллельные основанию конуса, делят его высоту на три равные части. Объём средней части конуса равен 14. Найдите объём всего конуса.

Answer 1

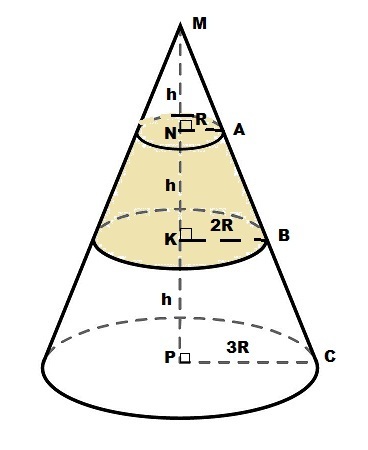
Пусть V₁ - объём верхнего конуса с высотой MN;
V₂ - объём конуса с высотой MK;
V₃ - объём конуса с высотой MP  - этот объём нужно найти
V₂ - V₁ = 14
По условию высота конуса MP разделена на три равных части
h = MN = NK = KP

ΔMKB ~ ΔMNA  подобны по двум углам: прямому и общему острому
$k_1 = frac{KB}{NA} = frac{MK}{MN} = frac{2h}{h} = 2$
Объёмы подобных фигур относятся как коэффициент подобия в кубе
$frac{V_2}{V_1} =k_1^3 = 2^3 = 8$
V₂ = 8V₁
По условию  V₂ - V₁ = 14
8V₁ - V₁ = 14    ⇒   7V₁ = 14   ⇒    V₁ = 2

ΔMPC ~ ΔMNA  -  подобны по двум углам: прямому и общему острому
$k_2 = frac{PC}{NA} = frac{MP}{MN} = frac{3h}{h} = 3$
$frac{V_3}{V_1} =k_2^3 = 3^3 = 27$
V₃ = 27V₁ = 27 * 2 = 54

Ответ: объём всего конуса равен 54