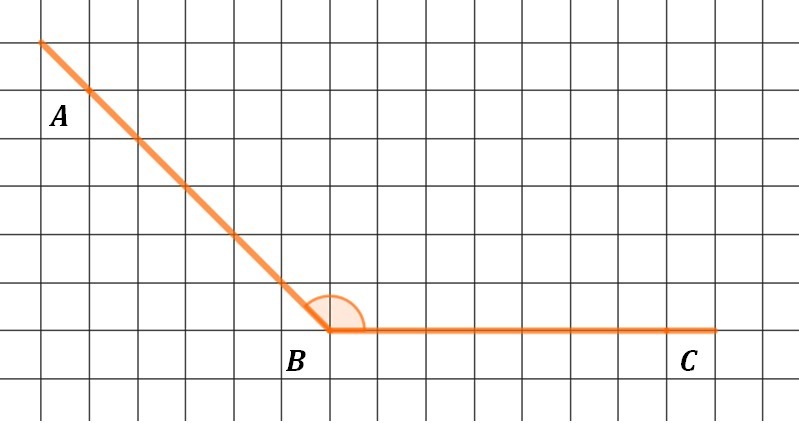
Найдите площадь пересечения угла ABC, изображённого на рисунке, с кругом радиуса 22/√π и центром в точке B.
Приложения:
Ответы
Ответ дал:
0
Так как луч ВА проведен по диагоналям клеточек, то
∠АВС = 90° + 45° = 135°.
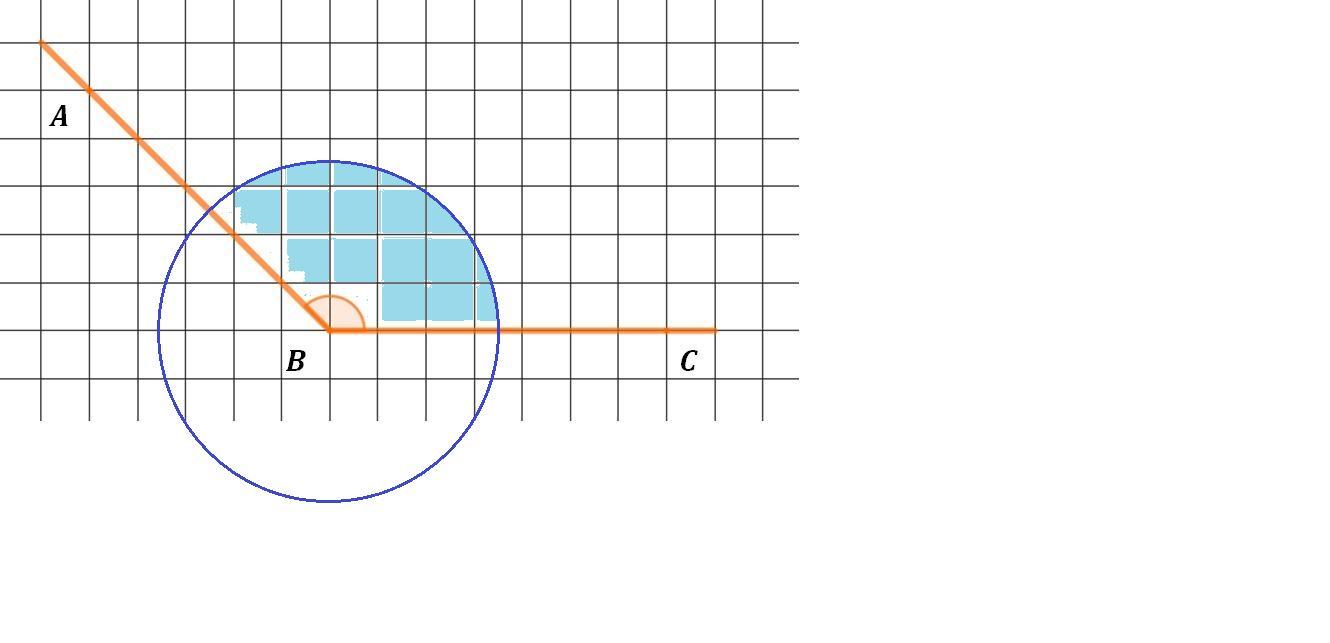
При пересечении угла с кругом получается сектор.
Площадь сектора:
Sсект = πR² · α / 360°
Sсект = π · (22/π)² · 135° / 360° = π · 484/π² · 3 / 8 =
= 121 · 3 / (2π) = 363 / (2π)
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад