Question

Пожалуйста помогите интеграл номер 1.5

Answer 1

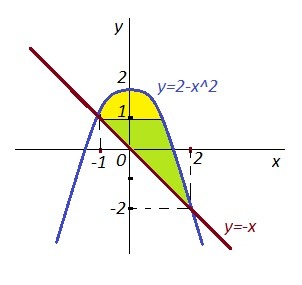
При дифференцировании с внешним интегралом по dх область D будет простой и точки входа в область лежат на линии  y= -x , а точки выхода - на линии у=2-х² . Область проектируется на ось ОХ в отрезок [-1.2] .
При дифференцировании с внешним интегралом по dy область D будет состоять из двух простых областей. У 1-ой области точки входа лежат на линии х=-у , а точки выхода на линии   $x=+sqrt{2-y}$  . Область проектируется на ось ОУ в отрезок [-1,2] .
У второй области точки входа и выхода лежат на параболе, но вход на левой её части  $x=-sqrt{2-y}$ , а выход на правой половине $x=+sqrt{2-y}$ . Область проектируется на ось ОУ в отрезок [1,2].
Точки пересечения параболы и прямой:

$x^2=2-y; ; to ; ; y=2-x^2\\x+y=0; ; to ; ; y=-x\\2-x^2=-x; ; to ; ; x^2-x-2=0; ,; ; x_1=-1; ,; ; x_2=2\\\ iintlimits_{D}, f(x,y), dx, dy= intlimits^2_{-1}, dxintlimits^{2-x^2}_{-x}f(x,y), dy=\\=intlimits^1_{-2}, dyintlimits^{sqrt{2-y}}_{-y}f(x,y), dx +intlimits^2_1 , dy intlimits^{sqrt{2-y}}_{-sqrt{2-y}} f(x,y) , dx$