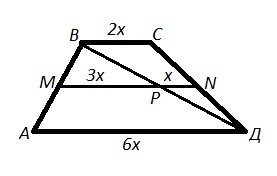
MN-средняя линия трапеции ABCD с основаниями BC и AC. Диагональ BD пересекает MN в точке P. Найдите длину меньшего основания BC, если MN=8, а MP:PN=3:1 .
Ответы
Ответ дал:
0
АВСД - трапеция.
MN - cредняя линия АВСД ⇒ РN - cредняя линия ΔВСД ⇒ ВС=2·PN .
MP:PN=3:1 ⇒ MP=3x , PN=x ⇒ MN=3x+x=4x=8 , x=2 , PN=2 .
BC=2·PN=2·2=4
MN - cредняя линия АВСД ⇒ РN - cредняя линия ΔВСД ⇒ ВС=2·PN .
MP:PN=3:1 ⇒ MP=3x , PN=x ⇒ MN=3x+x=4x=8 , x=2 , PN=2 .
BC=2·PN=2·2=4
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад