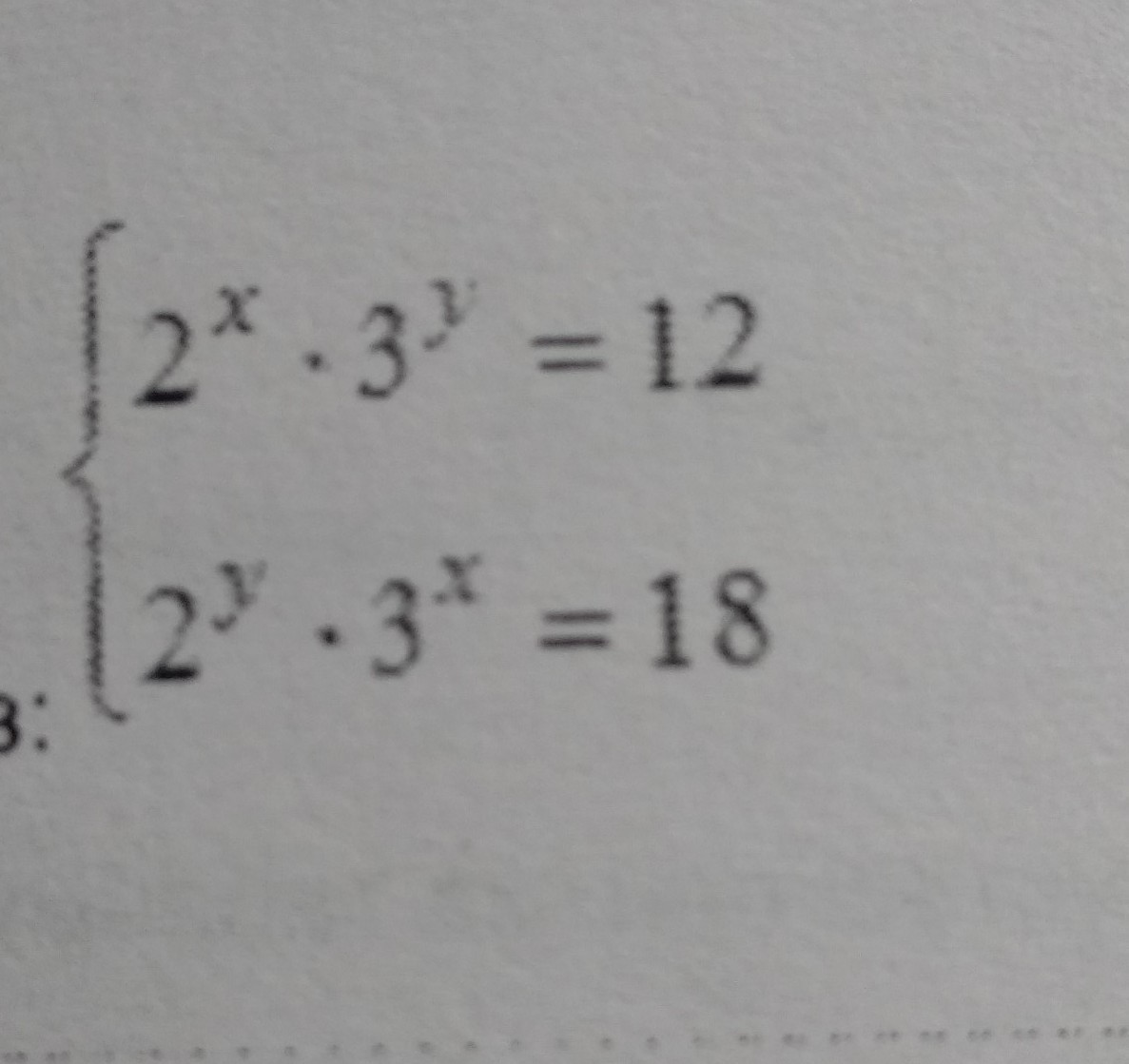Ответы
Ответ дал:
0
Решение:

Умножим почленно левые и правые части уравнений, получим:




Разделим почленно левые и правые части второго и первого уравнения, получим:





Составим и решим систему линейных уравнений:




Ответ: (2;1)
Умножим почленно левые и правые части уравнений, получим:
Разделим почленно левые и правые части второго и первого уравнения, получим:
Составим и решим систему линейных уравнений:
Ответ: (2;1)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад