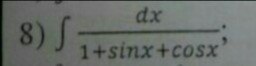Ответы
Ответ дал:
0
Как Вам было сказано:
делаем универсальную тригонометрическую подстановку:

Интеграл тогда принимает вид:

и возвращаемся к х:

делаем универсальную тригонометрическую подстановку:
Интеграл тогда принимает вид:
и возвращаемся к х:
Вас заинтересует
2 года назад
2 года назад
9 лет назад
9 лет назад
10 лет назад