Найдите область определения функции:
(если можно подробно!)
f(x)=(0,7)^{frac{1}{sqrt{x^{2}+7x+1}}}
Приложения:
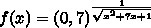
Ответы
Ответ дал:
0
нужно чтобы выполнялось утверждение, что подкоренное выражение должно быть неотрицательным, но так как квадратный корень у нас в знаменателе, он не может быть равен нулю, поэтому получаем неравенство:
x^2+7x+1>0
x^2+7x+1=0
D=49-4=45
x1=(-7-3sqrt(5))/2
x2=(-7+3sqrt(5))/2
(x-(-7-3sqrt(5))/2)*(x-(-7+3sqrt(5))/2)>0
решаем неравенство методом интервалов
++++++++++____________--------------____________++++++++++++++
(-7-3sqrt(5))/2) (-7+3sqrt(5))/2)
Ответ: x∈(-∞;-3,5-1,5sqrt(5))∪(-3,5+1,5sqrt(5);+∞)
x^2+7x+1>0
x^2+7x+1=0
D=49-4=45
x1=(-7-3sqrt(5))/2
x2=(-7+3sqrt(5))/2
(x-(-7-3sqrt(5))/2)*(x-(-7+3sqrt(5))/2)>0
решаем неравенство методом интервалов
++++++++++____________--------------____________++++++++++++++
(-7-3sqrt(5))/2) (-7+3sqrt(5))/2)
Ответ: x∈(-∞;-3,5-1,5sqrt(5))∪(-3,5+1,5sqrt(5);+∞)
Вас заинтересует
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад