Question

В правильной треугольной пирамиде сторона основания равна 6, а высота – 4. Найдите:

апофему пирамиды;
площадь боковой поверхности пирамиды.

Answer 1

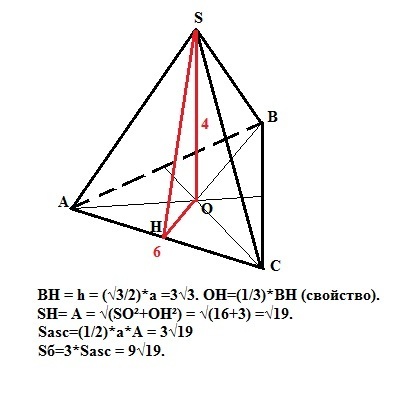
Высота правильного треугольника находится по формуле h=(√3/2)*a, где "а" - сторона треугольника.
h=(√3/2)*6 = 3√3.
В правильном треугольнике высота = медиана = биссектриса. Значит она делится в отношении 2:1, считая от вершины.
Тогда (1/3)*h - это проекция апофемы на основание = √3.
Апофема равна по Пифагору A= √(h²+(√3)²) = √19.
Площадь боковой грани Sг=(1/2)*a*A = 3√19.
Площадь боковой поверхности Sб=3*Sг =9√19.