Ответы
Ответ дал:
0
Линейная функция вида у=кх+в. График - прямая.
При к>0 прямая идет вверх при увеличении х. Например: у=2х или у=2х+5.
Ф-ция у=2х при в=0 проходит через начало координат, идет из 3 в 1 четверть. у=2х+5 проходит параллельно у=2х, но на 5 клеток выше.
Соответственно у=2х-4 на 4 клетки ниже. Если к у ф-ций равны, они параллельны.
При к<0 прямая идет вниз. При в=0 у=(-1/2)*х идет через начало координат из 2 в 4 четверть. При в>0 у=(-1/2)*х+2 прямая идет параллельно у=(-1/2)*х, но на 2 клетки выше. При в<0 у=(-1/2)*х-3 на 3 клетки ниже. Прямые у=-0,5х+8; у=-0,5х+11; у=-0,5х; у=-0,5х-6 все параллельны (к у всех=-0,5).
При к=0 у=в, например у=1; у=-7; у=12. Это все прямые параллельные оси ох. Они пересекают ось оу в точках 1; -7; 12.
у=0 - это прямая, совпадающая с осью ох. Для первых трех смотри фото. Не загружается.
При к>0 прямая идет вверх при увеличении х. Например: у=2х или у=2х+5.
Ф-ция у=2х при в=0 проходит через начало координат, идет из 3 в 1 четверть. у=2х+5 проходит параллельно у=2х, но на 5 клеток выше.
Соответственно у=2х-4 на 4 клетки ниже. Если к у ф-ций равны, они параллельны.
При к<0 прямая идет вниз. При в=0 у=(-1/2)*х идет через начало координат из 2 в 4 четверть. При в>0 у=(-1/2)*х+2 прямая идет параллельно у=(-1/2)*х, но на 2 клетки выше. При в<0 у=(-1/2)*х-3 на 3 клетки ниже. Прямые у=-0,5х+8; у=-0,5х+11; у=-0,5х; у=-0,5х-6 все параллельны (к у всех=-0,5).
При к=0 у=в, например у=1; у=-7; у=12. Это все прямые параллельные оси ох. Они пересекают ось оу в точках 1; -7; 12.
у=0 - это прямая, совпадающая с осью ох. Для первых трех смотри фото. Не загружается.
Приложения:
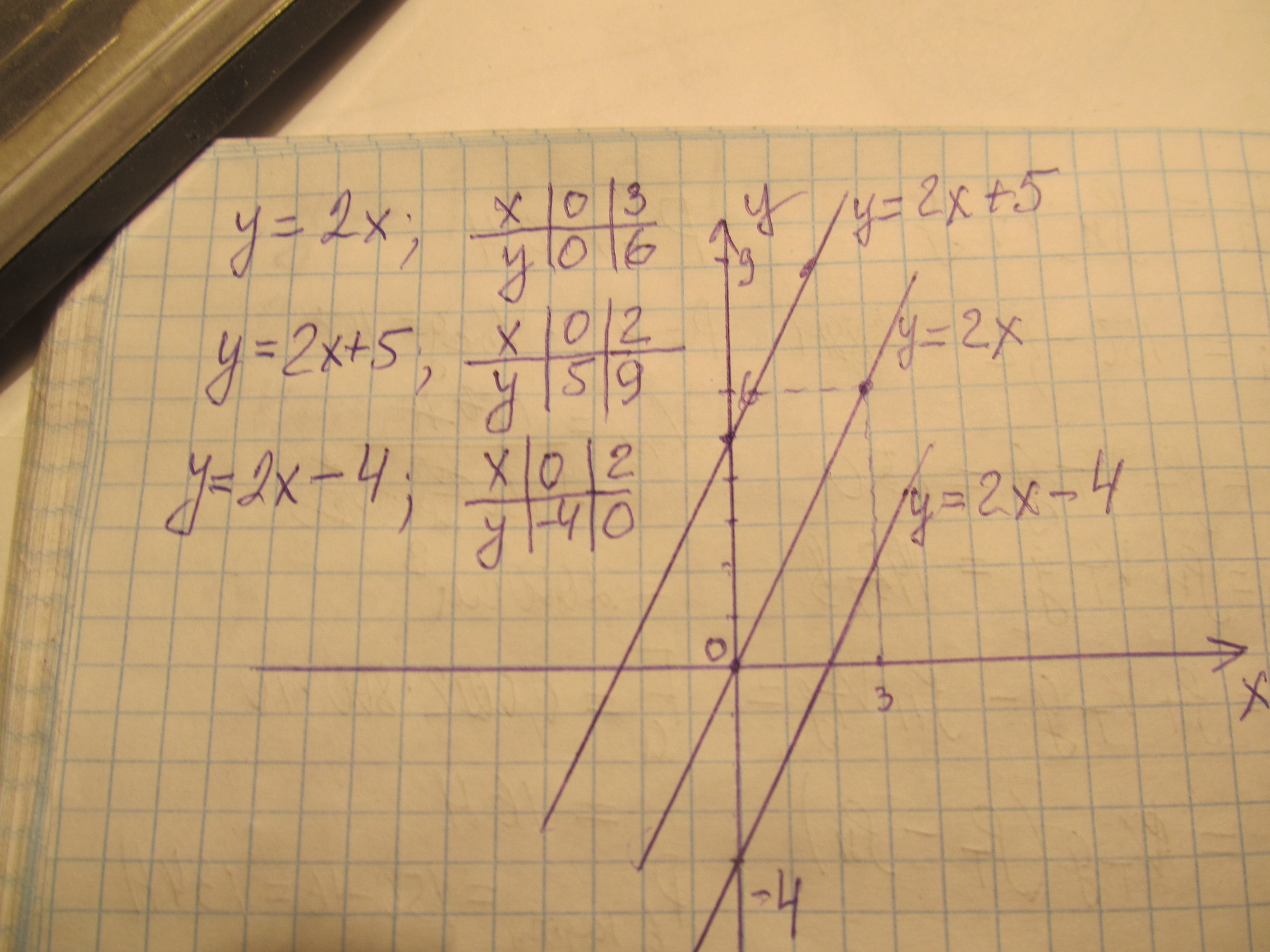
Ответ дал:
0
Прямая строится по 2-м точкам, надо почертить, чтобы все самому увидеть и привыкнуть. При построении сначала берем х=0, подставляем в формулу, получаем у точки. Потом любое значение х и тоже подставляем в формулу. Пусть у=2х+1; при х=0 у=2*0+1=1; точка (0;1). При х=3 у=2*3+1=7; точка (3;7). Через эти две точки проводим прямую. Сравни с у=2х. Они идут параллельно, но у=2х+1 на единицу выше.
Ответ дал:
0
Фото не загрузилось. Наверное текст большой.
Ответ дал:
0
Прошло несколько часов и фото вылезло)))
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад