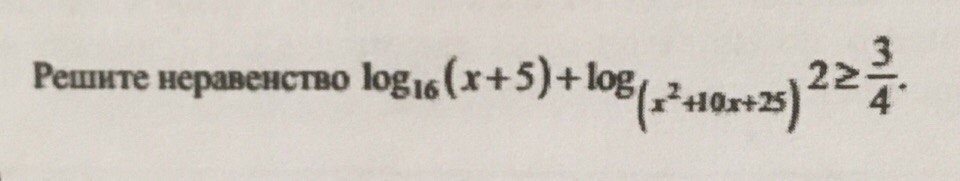Ответы
Ответ дал:
0
Начнём с ОДЗ

x∈(-5;-4)∪(-4;+∞)

Воспользуемся методом интервалов

А знаменатель просто выкалываем и получаем:
t∈(0;1/4]∪[1/2;+∞)
Хочу рассматривать отдельно ,у меня получится в первом интервале система ,а во втором простое неравенство

x∈(-4;3]∪[-1;+∞)
Теперь ищем пересечение с нашем ОДЗ и получается тоже самое ,что мы получили в конечном ответе
x∈(-5;-4)∪(-4;+∞)
Воспользуемся методом интервалов
А знаменатель просто выкалываем и получаем:
t∈(0;1/4]∪[1/2;+∞)
Хочу рассматривать отдельно ,у меня получится в первом интервале система ,а во втором простое неравенство
x∈(-4;3]∪[-1;+∞)
Теперь ищем пересечение с нашем ОДЗ и получается тоже самое ,что мы получили в конечном ответе
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад