Ответы

Ответ:
ВМ = 8
Объяснение:
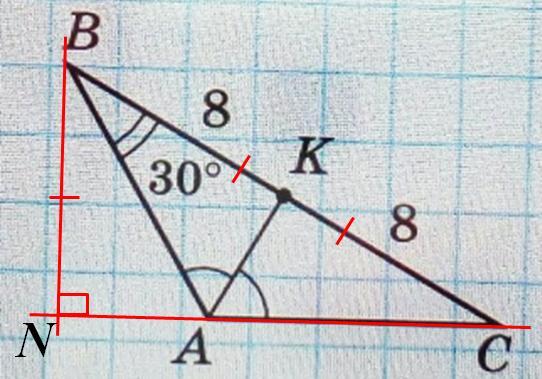
Смотри прикреплённый рисунок.
ВС = ВК + СК = 8 + 8 = 16
По условию АК - биссектриса и медиана.
Известно, что если в треугольнике биссектриса является и медианой, то треугольник равнобедренный. ΔАВС - равнобедренный и ∠С = ∠В = 30°.
Рассмотрим прямоугольный треугольник СВМ.
Катет ВМ лежит против ∠С = 30°. Значит, ВМ равен половине гипотенузы ВС.
ВМ = 0,5 ВС = 0,5 · 16 = 8

Ответ:
BN=8 (единиц)
Объяснение:
Дано: (см. рисунок)
В ∆ABC
∠B=30°
∠BAK=∠CAK
BK=KC=8
Найти: BN
Решение.
Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из данной точки к данной прямой, в нашем случае отрезок BN.
По условию в ∆ABC: BK=KC и ∠BAK=∠KAC, тогда AK является и медианой и биссектрисой, следовательно, по свойству треугольников ∆ABC равнобедренный и AK есть и высота. Отсюда:
∠B=∠C=30°, ∠BKA=90°, в ∆ABK:
∠BAK=∠KAC=180°–90°–30°=60° и ∠A=60°+60°=120°.
Но тогда ∠BAN=180°–120°=60° и ∠ABN=90°–60°=30°.
Так как AB – общая сторона и прилегающие углы ∠BAN=∠BAK=60°, ∠ABK=∠ABN=30°, то по второму признаку треугольников ∆ABK и ∆ABN равны! Тогда BN=BK=8.