Question

на клеточной бумаге из точки А проведите касательные к данной окружности (рис 19.6)

Answer 1

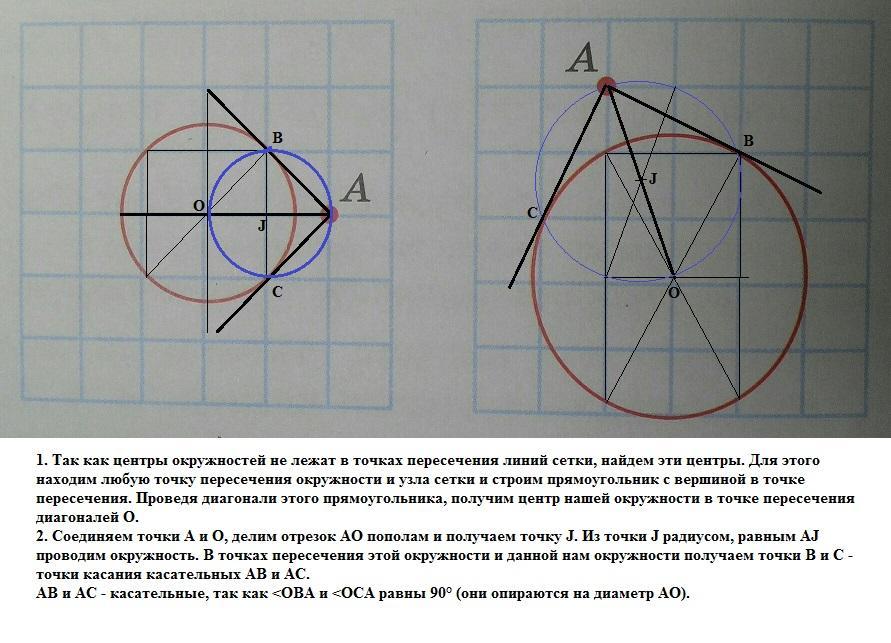
1. Так как центры окружностей не лежат в точках пересечения линий сетки, найдем эти центры. Для этого находим любую точку пересечения окружности и узла сетки и строим прямоугольник с вершиной в точке пересечения. Проведя диагонали этого прямоугольника, получим центр нашей окружности в точке пересечения диагоналей О.

2. Соединяем точки А и О, делим отрезок АО пополам и получаем точку J. Из точки J радиусом, равным АJ проводим окружность. В точках пересечения этой окружности и данной нам окружности получаем точки В и С - точки касания касательных АВ и АС.

АВ и АС - касательные, так как <OBA и <OCA равны 90° (они опираются на диаметр АО).