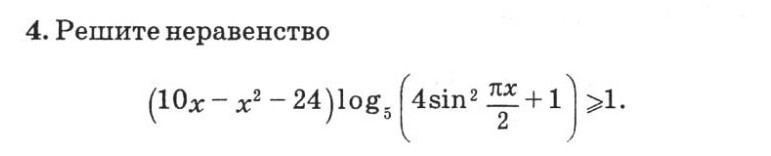Ответы
Ответ дал:
0
Оценим каждый множитель в отдельности:
10x - x² - 24 = - x² + 10x - 24 = -(x² - 10x + 25) + 1 = 1 - ( x - 5 )²
Выражение 1 - (x - 5)² ≤ 1

Получили что первый множитель ≤ 1 , а второй множитель больше нуля но меньше единицы. Но при этих условиях произведение двух множителей будет ≥ 1 только в случае, когда и первый и второй множители равны 1, то есть
1) 10x - x² - 24 = 1
- x² + 10x - 25 = 0
x² - 10x + 25 = 0
(x - 5)² = 0
x - 5 = 0
x = 5
2)

-верно
Значение x = 5 является решением и этого уравнения.
Значит это единственное решение неравенства.
10x - x² - 24 = - x² + 10x - 24 = -(x² - 10x + 25) + 1 = 1 - ( x - 5 )²
Выражение 1 - (x - 5)² ≤ 1
Получили что первый множитель ≤ 1 , а второй множитель больше нуля но меньше единицы. Но при этих условиях произведение двух множителей будет ≥ 1 только в случае, когда и первый и второй множители равны 1, то есть
1) 10x - x² - 24 = 1
- x² + 10x - 25 = 0
x² - 10x + 25 = 0
(x - 5)² = 0
x - 5 = 0
x = 5
2)
-верно
Значение x = 5 является решением и этого уравнения.
Значит это единственное решение неравенства.
Ответ дал:
0
Какая красота!!!)) Спасибо огромное)))))))
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад