Question

Решите пожалуйста с разъяснением!

Answer 1

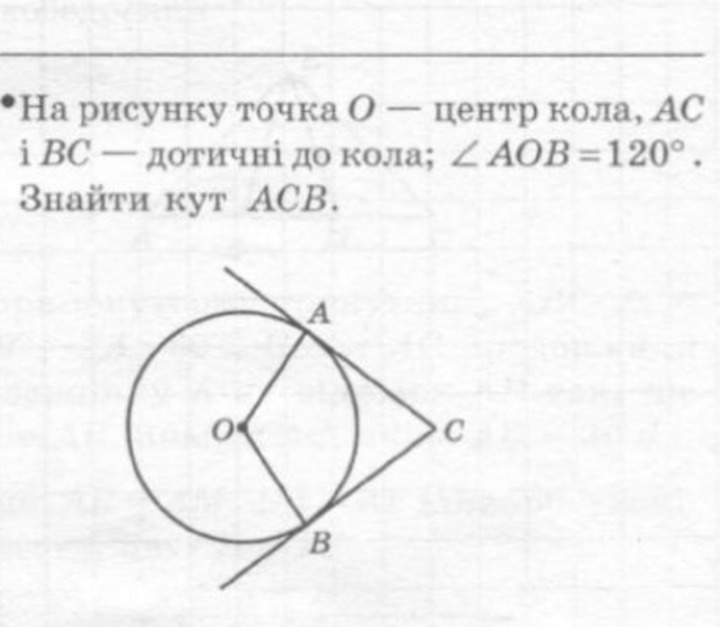
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. 
∠OAC=90°, ∠OBC =90°

Сумма углов четырехугольника равна 360°.
ACBO: ∠ACB= 360°-∠OAC-∠OBC-∠AOB = 360°-90°·2-120° =60°

Answer 2

Спасибо за решение но мы ещё не изучали четырёхугольники

Answer 3

Тогда проведем OC. △AOC=△BOC (по катетам (радиусы) и общей гипотенузе). ∠ACО=∠BCO, ∠AOC=∠BOC. ∠ACO=90°-∠AOC (сумма острых углов прямоугольного треугольника 90°). ∠ACB=2∠ACO=2(90°-∠AOC)=180°-2∠AOC=180°-∠AOB

Answer 4

Спасибо